b01lersCTF 2024 Writeup
This weekend (Apr 12-14, 2024), I was honored to work with such great people as a b01lers CTF challenge author. It was my first time writing CTF challenges. I learned a lot, arguably even more than I usually do as a CTF participant, not only through the process of making the challenges but also as an organizer and from some rookie mistakes that I made (will elaborate later). It was an interesting and invaluable experience, and I am looking forward to the next year's b01lers CTF already.
As a challenge author, I suppose I am semi-obligated to release the intented solutions to my challenges. This writeup exists to fulfill that responsibility. I will describe each challenge and my solution in detail, as well as some selected solutions by participants that I find beautiful (I mean solution, not participants).
Before I start, I want to give a huge thanks to the b01lers president (CaptainNapkins), team officers and fellow challenge authors for this opportunity and making b01lers CTF go smooth!
Crypto
half-big-rsa
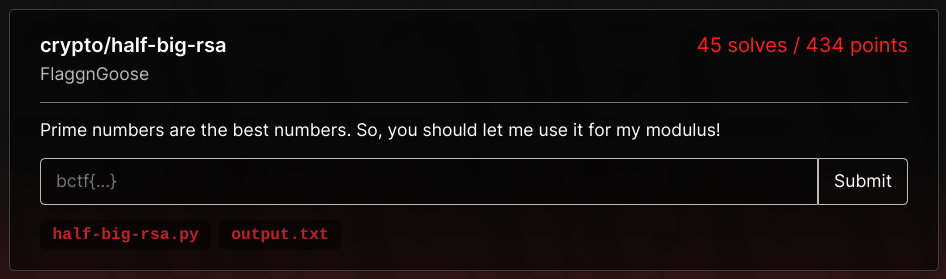
## half-big-rsa.py
import math
from Crypto.Util.number import getPrime, bytes_to_long, long_to_bytes
import os
num_bits = 4096
e = (num_bits - 1) * 2
n = getPrime(num_bits)
with open("flag.txt","rb") as f:
flag = f.read()
m = bytes_to_long(flag)
c = pow(m, e, n)
print(c)
with open("output.txt", "w") as f:
f.write("e = {0}\n".format(e))
f.write("n = {0}\n".format(n))
f.write("c = {0}\n".format(c))## output.txt
e = 8190
n = 665515140120452927777672138241759151799589898667434054796291409500701895847040006534274017960741836352283431369658890777476904763064058571375981053480910502427450807868148119447222740298374306206049235106218160749784482387828757815767617741823504974133549502118215185814010416478030136723860862951197024098473528800567738616891653602341160421661595097849964546693006026643728700179973443277934626276981932233698776098859924467510432829393769296526806379126056800758440081227444482951121929701346253100245589361047368821670154633942361108165230244033981429882740588739029933170447051711603248745453079617578876855903762290177883331643511001037754039634053638415842161488684352411211039226087704872112150157895613933727056811203840732191351328849682321511563621522716119495446110146905479764695844458698466998084615534512596477826922686638159998900511018901148179784868970554998882571043992165232556707995154316126421679595109794273650628957795546293370644405017478289280584942868678139801608538607476925924119532501884957937405840470383051787503858934204828174270819328204062103187487600845013162433295862838022726861622054871029319807982173856563380230936757321006235403066943155942418392650327854150659087958008526462507871976852849
c = 264114212766855887600460174907562771340758069941557124363722491581842654823497784410492438939051339540245832405381141754278713030596144467650101730615738854984455449696059994199389876326336906564161058000092717176985620153104965134542134700679600848779222952402880980397293436788260885290623102864133359002377891663502745146147113128504592411055578896628007927185576133566973715082995833415452650323729270592804454136123997392505676446147317372361704725254801818246172431181257019336832814728581055512990705620667354025484563398894047211101124793076391121413112862668719178137133980477637559211419385463448196568615753499719509551081050176747554502163847399479890373976736263256211300138385881514853428005401803323639515624537818822552343927090465091651711036898847540315628282568055822817711675290278630405760056752122426935056309906683423667413310858931246301024309863011027878238814311176040130230980947128260455261157617039938807829728147629666415078365277247086868327600962627944218138488810350881273304037069779619294887634591633069936882854003264469618591009727405143494184122164870065700859379313470866957332849299246770925463579384528152251689152374836955250625216486799615834558624798907067202005564121699019508857929778460To begin with, we are given the equation $c = m^e \text{ mod } n$ where $n$ is a 4096-bit prime number. Normally, we'd be able to compute $d := e^{-1} \text{ mod } n-1$ and find $m$ by computing $c^d \text{ mod } n$, but unfortunately $e^{-1} \text{ mod } n-1$ does not exist as $g := \gcd(e, n-1) = 18 \neq 1$.
Fortunately, we have $\gcd(e/g, n-1) = 1$, so $d_1 := (e/g)^{-1} \text{ mod } n-1$ exists. That is, there exists $k \in \mathbb{Z}$ such that
\[ \frac{e}{g} d_1 = (n-1) k + 1 \implies e d_1 = (n-1)gk + g \]and hence, $c^{d_1} = m^{e d_1} = m^g = m^{18} \text{ mod } n$. Denote $m_1 := m^{g} \text{ mod } n$. It is clear that $m_1^{e/g} = c \text{ mod } n$.
with open("output.txt","rb") as f:
file = f.readlines()
e = int((file[0])[4:])
n = int((file[1])[4:])
c = int((file[2])[4:])
g = math.gcd(e, n-1)
# math.gcd(e//g, n-1)
d1 = pow(e//g, -1, n-1)
m1 = pow(c, d1, n)
assert pow(m1, e//g, n) == c # TrueWe are left with taking 18-th roots of $m_1$ in $\mathbb{F}_n$. We could use nth_root function in sagemath, but given that $n$ is a 4096-bit prime, it'd take forever. Let's use some trick. Factordb says:
Since $g = 18 = 2 \times 3^2$, we have $\gcd(g, (n-1)/g) = 6$, but
\[ \gcd\left(24 g, \frac{n-1}{24 g} \right) = 1 \]because $24g = 2^4 \times 3^3$. So, we can raise $m_1$ to the power of $24$,
\[ m_2 := (m_1)^{24} = m^{24g} \mod n \]and compute the inverse of $24g$ -- there exists $k' \in \mathbb{Z}$ such that
\begin{align*} d_2 := (24g)^{-1} \text{ mod } \frac{n-1}{24 g} & \implies 24 g d_2 = 1 + \frac{n-1}{24 g} k' \\ & \implies 24 g \cdot (24 g\; d_2) = 24g + (n-1)k' \end{align*}Hence,
\begin{align*} (m_2)^{24g d_2} = m^{24g \cdot (24g d_2)} = m^{24g} \mod n \end{align*}assert math.gcd(24 * g, (n-1)//(24 * g)) == 1 # True
m2 = pow(m1, 24, n)
d2 = pow(24 * g, -1, (n-1)//(24 * g))
m_candidate = pow(m2, d2, n)
assert pow(m_candidate, 24 * g, n) == m2 # Trueand therefore, $m$ would be one of the $24g$-th roots of $(m_2)^{24g d_2}$ in $\mathbb{F}_n$. That is, let $\rho$ be a $24g$-th root of unity in $\mathbb{F}_n$, then $m = (m_2)^{d_2} \rho^i \text{ mod } n$ for some integer $i$.
This can be done by finding a generator of a subgroup $E$ of order $24g = 432$ in $\mathbb{F}_n^\times$. Note that $E$ is cyclic since $n$ is prime. This can be done brute forcefully but in most cases (and apparently and fortunately, for this case as well) it should finish very quickly.
# Find a subgroup E with order 432 in F_n^*
gen_ind = 1
gen_E = 1 # generator of E
# 432 = 2^4 * 3^3
# Exclude the elements whose 2^4, 3^3, 2^3 * 3^3, or 2^4 * 3^2 power is 1
# Their factors form the factors of 432.
while gen_E == 1 or pow(gen_E, 16, n) == 1 or pow(gen_E, 27, n) == 1 \
or pow(gen_E, 144, n) == 1 or pow(gen_E, 216, n) == 1:
gen_ind += 1
gen_E = pow(gen_ind, (n-1) // (24 * g), n)
# Testing to make sure g_E is order 432
for i in range(24 * g + 1):
if i != 0 and i != 24 * g:
assert pow(gen_E, i, n) != 1We are then left with computing the said $(m_2)^{d_2} \rho^i \text{ mod } n$ for $i = 0,1,\dots, 24g-1$.
for i in range(0, 24 * g):
m = (m_candidate * pow(gen_E, i, n)) % n
if pow(m, e, n) == c and b'bctf{' in long_to_bytes(m):
print(long_to_bytes(m))
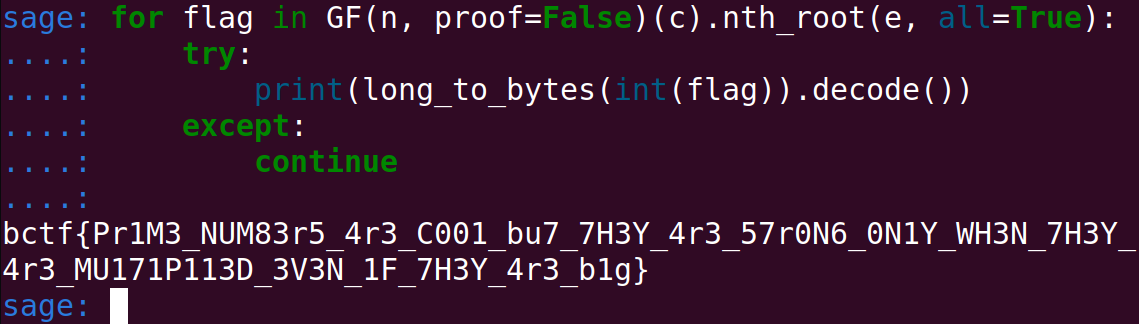
## b'bctf{Pr1M3_NUM83r5_4r3_C001_bu7_7H3Y_4r3_57r0N6_0N1Y_WH3N_
## 7H3Y_4r3_MU171P113D_3V3N_1F_7H3Y_4r3_b1g}'Flag: bctf{Pr1M3_NUM83r5_4r3_C001_bu7_7H3Y_4r3_57r0N6_0N1Y_WH3N_7H3Y_4r3_
MU171P113D_3V3N_1F_7H3Y_4r3_b1g}
The full solution script sol.py is provided below for the sake of completeness:
sol.py (Click to expand)
## sol.py
import math
from Crypto.Util.number import getPrime, bytes_to_long, long_to_bytes
import os
with open("output.txt","rb") as f:
file = f.readlines()
e = int((file[0])[4:])
n = int((file[1])[4:])
c = int((file[2])[4:])
g = math.gcd(e, n-1)
# math.gcd(e//g, n-1)
d1 = pow(e//g, -1, n-1)
m1 = pow(c, d1, n)
assert pow(m1, e//g, n) == c # True
assert math.gcd(24 * g, (n-1)//(24 * g)) == 1 # True
m2 = pow(m1, 24, n)
d2 = pow(24 * g, -1, (n-1)//(24 * g))
m_candidate = pow(m2, d2, n)
assert pow(m_candidate, 24 * g, n) == m2 # True
# Find a subgroup E with order 432 in F_n^*
gen_ind = 1
gen_E = 1 # generator of E
# 432 = 2^4 * 3^3
# Exclude the elements whose 2^4, 3^3, 2^3 * 3^3, or 2^4 * 3^2 power is 1
# Their factors form the factors of 432.
while gen_E == 1 or pow(gen_E, 16, n) == 1 or pow(gen_E, 27, n) == 1 \
or pow(gen_E, 144, n) == 1 or pow(gen_E, 216, n) == 1:
gen_ind += 1
gen_E = pow(gen_ind, (n-1) // (24 * g), n)
# Testing to make sure g_E is order 432
for i in range(24 * g + 1):
if i != 0 and i != 24 * g:
assert pow(gen_E, i, n) != 1
for i in range(0, 24 * g):
m = (m_candidate * pow(gen_E, i, n)) % n
if pow(m, e, n) == c and b'bctf{' in long_to_bytes(m):
print(long_to_bytes(m))
## b'bctf{Pr1M3_NUM83r5_4r3_C001_bu7_7H3Y_4r3_57r0N6_0N1Y_WH3N_
## 7H3Y_4r3_MU171P113D_3V3N_1F_7H3Y_4r3_b1g}'After the CTF ended, some participants noted me that using the nth_root function on Sagemath worked well for this challenge. One of them (ConnerM) shared their code with me, I tested it myself and apparently that was true (although it takes a few minutes)!
I guess I did not do a good job choosing the parameters. It might be interesting to study what parameters we should choose to frustrate such brute force attacks.
shamir-for-dummies
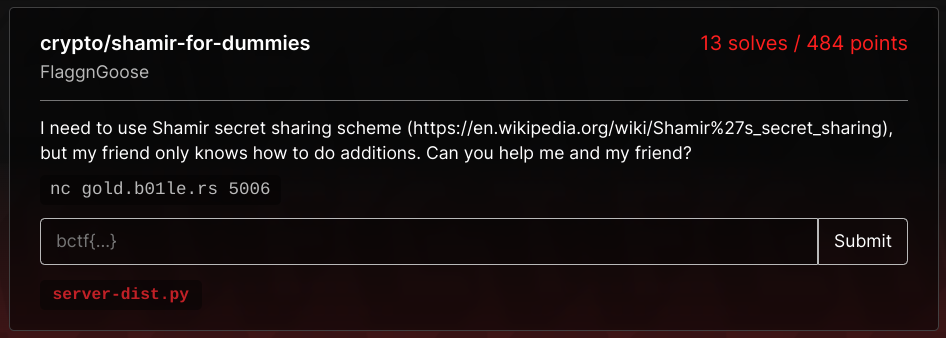
server-dist.py (Click to expand)
## server-dist.py
import os
import sys
import time
import math
import random
from Crypto.Util.number import getPrime, isPrime, bytes_to_long, long_to_bytes
def polynomial_evaluation(coefficients, x):
at_x = 0
for i in range(len(coefficients)):
at_x += coefficients[i] * (x ** i)
at_x = at_x % p
return at_x
flag = b'bctf{REDACTED}'
print("")
print("Thanks for coming in. I can really use your help.\n")
print("Like I said, my friend can only do additions. He technically can do division but he says he can only do it once a day.")
print("")
print("I need to share my secret using Shamir secret sharing. Can you craft the shares, in a way that my friend can recover it?\n")
print("")
print("Don't worry, I have the polynomial and I will do all the math for you.")
print("")
s = bytes_to_long(flag)
n = getPrime(4)
p = getPrime(512)
while p % n != 1:
p = getPrime(512)
print("Let's use \n")
print("n =", n)
print("k =", n)
print("p =", p)
print("")
coefficients = [s]
for i in range(1, n):
coefficients.append(random.randint(2, p-1))
print("Okay, I have my polynomial P(X) ready. Let me know when you are ready to generate shares with me.\n")
print("")
evaluation_points = []
shares = []
count = 1
while count < n+1:
print("Evaluate P(X) at X_{0} =".format(count))
print("> ", end="")
eval_point = int(input())
if eval_point % p == 0:
print("Lol, nice try. Bye.")
exit()
break
elif eval_point < 0 or eval_point > p:
print("Let's keep things in mod p. Please choose it again.")
else:
if eval_point not in evaluation_points:
evaluation_points.append(eval_point)
share = polynomial_evaluation(coefficients, eval_point)
shares.append(share)
count += 1
else:
print("You used that already. Let's use something else!")
print("Nice! Let's make sure we have enough shares.\n")
assert len(shares) == n
assert len(evaluation_points) == n
print("It looks like we do.\n")
print("By the way, would he have to divide with anything? (Put 1 if he does not have to)")
print("> ", end="")
some_factor = int(input())
print("Good. Let's send those over to him.")
for _ in range(3):
time.sleep(1)
print(".")
sys.stdout.flush()
sum_of_shares = 0
for s_i in shares:
sum_of_shares += s_i
sum_of_shares = sum_of_shares % p
sum_of_shares_processed = (sum_of_shares * pow(some_factor, -1, p)) % p
if sum_of_shares_processed == s:
print("Yep, he got my secret message!\n")
print("The shares P(X_i)'s were':")
print(shares)
print("... Oh no. I think now you'd know the secret also... Thanks again though.")
else:
print("Sorry, it looks like that didn't work :(")This is a Shamir's secret sharing (SSS) problem. Suppose that $n$ parties want to share a secret $s \in \mathbb{F}$ where $\mathbb{F}$ is a field, with reconstruction threshold $k \leq n$ (i.e., any group of $k-1$ parties or less has no access to $s$, but $k$ parties or more has). Central authority (i.e., whoever possesses the secret $s$) samples a polynomial $p(X) \in \mathbb{F}[X]/(X^k)$ of degree $k-1$ randomly given $p(0) = s$. Then it chooses the evaluation points $\alpha_1, \alpha_2, \dots, \alpha_n \in \mathbb{F}$, computes and sends the $i$-th share of the secret $s_i := p(\alpha_i)$ to the $i$-th party. By Fundamental theorem of Algebra, $p(X)$ can be uniquely determined only when $k$ or more points $(\alpha_i, p(\alpha_i))$ are given. The security is guaranteed only when $\mathbb{F}$ is a finite field, which in our problem would be $\mathbb{F}_p$ for some given prime $p$. I recommend the readers to refer to this Wikipedia article for further details.
server-dist.py file might be a bit long, but in reality, there are only a few lines where we need to pay attention to.
## From server-dist.py
print("n =", n)
print("k =", n)
...
print("Evaluate P(X) at X_{0} =".format(count))
...
eval_point = int(input())
...
evaluation_points.append(eval_point)
share = polynomial_evaluation(coefficients, eval_point)
shares.append(share)
...
some_factor = int(input())
...
for s_i in shares:
sum_of_shares += s_i
sum_of_shares = sum_of_shares % p
sum_of_shares_processed = (sum_of_shares * pow(some_factor, -1, p)) % pFirst, the server knows the secret $s$ (obviously), sets $n = k$, and they are sampling the polynomial $p(X) \in \mathbb{F}_p[X]/(X^{n})$ of degree $n-1$. Second, they lets you choose the evaluation places $\alpha_i$'s for all $i = 1,2,\dots, n$. Third, you have to choose them wisely so that the sum of all shares $p(\alpha_i)$'s is a multiple of the secret.
Let $p(X) = s + c_1 X + c_2 X^2 + \cdots + c_{n-1} X^{n-1}$ where $c_1, \dots, c_{n-1} \in \mathbb{F}_p$. Let $\alpha_i$'s be evaluation places. Then,
\begin{align*} \sum_{i=1}^n p(\alpha_i) & = s + c_1 \alpha_1 + c_2 \alpha_1^2 + \cdots + c_{n-1} \alpha_1^{n-1} \\ & \qquad + s + c_1 \alpha_2 + c_2 \alpha_2^2 + \cdots + c_{n-1} \alpha_2^{n-1} \\ & \qquad + \cdots \\ & \qquad + s + c_1 \alpha_n + c_2 \alpha_n^2 + \cdots + c_{n-1} \alpha_n^{n-1} \\ & = ns + c_1 \sum_{i=1}^n \alpha_i + c_2 \sum_{i=1}^n \alpha_i^2 + \cdots + c_{n-1} \sum_{i=1}^n \alpha_{i}^{n-1} \end{align*}So if we can find $\alpha_i$'s such that those sums all get canceled to $0 \text{ mod } p$, we are done. The first sum $\sum_{i=1}^n \alpha_i$ is exactly $0$ if $\alpha_i = \omega^i$ where $\omega$ is a non-trivial $n$-th root of unity in modulo $p$.
\begin{align*} \sum_{i=1}^n \alpha_i & = \omega + \omega^2 + \cdots + \omega^{n-1} + \omega^n \\ & = 1 + \omega + \omega^2 + \cdots + \omega^{n-1} \\ & = \frac{(1-\omega)(1 + \omega + \omega^2 + \cdots + \omega^{n-1})}{1-\omega} \\ & = \frac{1-\omega^n}{1-\omega} \\ & = 0 \mod p \end{align*}because $\omega^n = 1 \text{ mod } p$. It is easy to see that the second sum $\sum_{i=1}^n \alpha_i^2$ is also $0 \text{ mod } p$ by the same process
\begin{align*} \sum_{i=1}^n \alpha_i^2 & = \omega^2 + (\omega^2)^2 + \cdots + (\omega^{n-1})^2 + (\omega^n)^2 \\ & = 1 + \omega^2 + (\omega^2)^2 + \cdots + (\omega^{n-1})^2 \\ & = \frac{(1-\omega^2)(1 + \omega^2 + (\omega^2)^2 + \cdots + (\omega^{n-1})^2)}{1-\omega^2} \\ & = \frac{1-\omega^{2n}}{1-\omega^2} \\ & = 0 \mod p \end{align*}One way to generalize this is to view $\omega^2$ as another $n$-root of unity in mod $p$. Hence, by this logic, we can conclude that all sums $\sum_{i=1}^n \alpha_i, \dots, \sum_{i=1}^n \alpha_i^{n-1}$ are $0 \text{ mod } p$.
We are then left with just $ns \text{ mod } p$, which we can just have them divide it by $n$.
## sol.py
import os
import sys
import time
import math
import random
from Crypto.Util.number import bytes_to_long, long_to_bytes
import pwn
def nth_root_of_unity(n, p):
gen_ind = 1
gen_E = 1 # generator of E
while gen_E == 1:
gen_ind += 1
gen_E = pow(gen_ind, (p-1) // n, p)
assert pow(gen_E, n, p) == 1
sum_omega_i = 0
for i in range(0, n):
sum_omega_i += pow(gen_E, i, p)
assert (sum_omega_i % p) == 0
return gen_E
nc_ed = pwn.remote('gold.b01le.rs', '5006')
nc_ed.recvuntil("n = ")
n = int(nc_ed.recvline())
nc_ed.recvuntil("p = ")
p = int(nc_ed.recvline())
for i in range(1, n+1):
nc_ed.recvuntil("> ")
nc_ed.sendline(str(pow(nth_root_of_unity(n, p), i, p)))
nc_ed.recvuntil("> ")
nc_ed.sendline(str(n))
# nc_ed.interactive()
nc_ed.recvuntil("The shares P(X_i)'s were':\n")
shares = nc_ed.recvline()
shares = str(shares, encoding='utf-8')
shares = (shares[1:])[:-2] # removing brackets and "\n"
# print("sol.py got shares as =", shares)
share_list = shares.split(", ")
# print(share_list)
sum_shares = 0
for s_i in share_list:
sum_shares += int(s_i)
sum_shares %= p
sum_shares = (sum_shares * pow(n, -1, p)) % p
print(long_to_bytes(sum_shares))
### b'bctf{P0LYN0m14l_1N_M0d_P_12_73H_P0W3Rh0u23_0F_73H_5h4M1r}'Flag: bctf{P0LYN0m14l_1N_M0d_P_12_73H_P0W3Rh0u23_0F_73H_5h4M1r}
This challenge was inspired by Maji et al.'s EuroCrypt '21 (see Remark 1) and Maji et al.'s ITC '22 (see Theorem 5) papers on an example attack against Shamir secret sharing scheme when evaluation places for the polynomial are chosen poorly.
R(esurre)C(tion)4
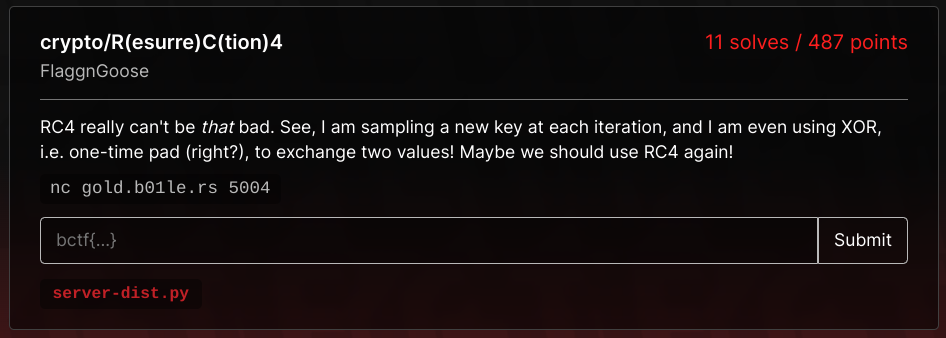
server-dist.py (Click to expand)
import random
from Crypto.Util.number import getPrime, isPrime, bytes_to_long, long_to_bytes
"""
Key-scheduling algorithm (KSA)
"""
def KSA(key):
S = [i for i in range(0, 256)]
i = 0
for j in range(0, 256):
i = (i + S[j] + key[j % len(key)]) % 256
S[i] ^= S[j] ## swap values of S[i] and S[j]
S[j] ^= S[i]
S[i] ^= S[j]
return S
"""
Pseudo-random generation algorithm (PRGA)
"""
def PGRA(S):
i = 0
j = 0
while True: ## while GeneratingOutput
i = (1 + i) % 256
j = (S[i] + j) % 256
S[i] ^= S[j] ## swap values of S[i] and S[j]
S[j] ^= S[i]
S[i] ^= S[j]
yield S[(S[i] + S[j]) % 256]
if __name__ == '__main__':
FLAG = 'bctf{REDACTED}'
print("Would you like to pad the plaintext before encrypting it?")
print("(Just hit enter if you do not want to add any padding(s).)")
Padding = input()
input_text = ''
input_text += Padding
input_text += FLAG
plaintext = [ord(char) for char in input_text]
key = long_to_bytes(random.getrandbits(2048)) # 2048 bits = 256 bytes
key = [byte for byte in key]
S = KSA(key)
keystream = PGRA(S)
ciphertext = ''
for char in plaintext:
enc = char ^ next(keystream)
enc = (str(hex(enc)))[2:]
if len(enc) == 1: ## make sure they are all in the form 0x**
enc = '0' + enc
ciphertext += enc
print(ciphertext)This is a well-known insecure implementation of RC4. The only part that you need to pay attention to is the following:
### From server-dist.py
S[i] ^= S[j] ## swap values of S[i] and S[j]
S[j] ^= S[i]
S[i] ^= S[j]Logically, this is equivalent to:
temp = S[i]
S[i] = S[j]
S[j] = tempbut implementation-wise, it is not. If you are swapping two values via XOR operation like server-dist.py does, if the two values are the same, then they both end up becoming a $0$ as the XOR of two same numbers is equal to $0$.
If the plaintext is long---like very long---then we are certainly bound to reach a point where S[i] = S[j] (and/or i = j). Once this happens, as said above, S will be updated as S[i] = S[j] = 0, and this will be 'accumulated' and eventually transform S into a sequence of zeroes, which leaves (some parts of) the plaintext unencrypted. Therefore, our goal is to just make the plaintext very long by padding it with a bunch of garbage data or empty characters/spaces, so the plaintext appears at the end of the ciphertext.
import pwn
import binascii
nc_ed = pwn.remote('gold.b01le.rs', '5004')
nc_ed.recvuntil("padding(s).)")
padding = ' ' * 1000000
nc_ed.sendline(padding)
nc_ed.recvline() ## Empty line
ciphertext = nc_ed.recvline() ## b'...\n'
ciphertext = str(ciphertext)[2:-3] ## Remove " b' " and " \n' "
unhexed_ct = binascii.unhexlify(ciphertext)
# print(unhexed_ct) ## This is also correct but it's too long
## Since flag won't be that long anyway, just print the last 50 chars.
print(unhexed_ct[len(unhexed_ct) - 50:len(unhexed_ct)])
## bctf{1f_gOOgL3_541D_1T_15_b4D_Th3n_1T_15_b4D}Flag: bctf{1f_gOOgL3_541D_1T_15_b4D_Th3n_1T_15_b4D}
This challenge was inspired by the closing keynote talk (titled "Where Code Meets Chip") at the 2024 Annual CERIAS Security Symposium, given by Philippe Biondi from Airbus.
Misc
basketball-scholar
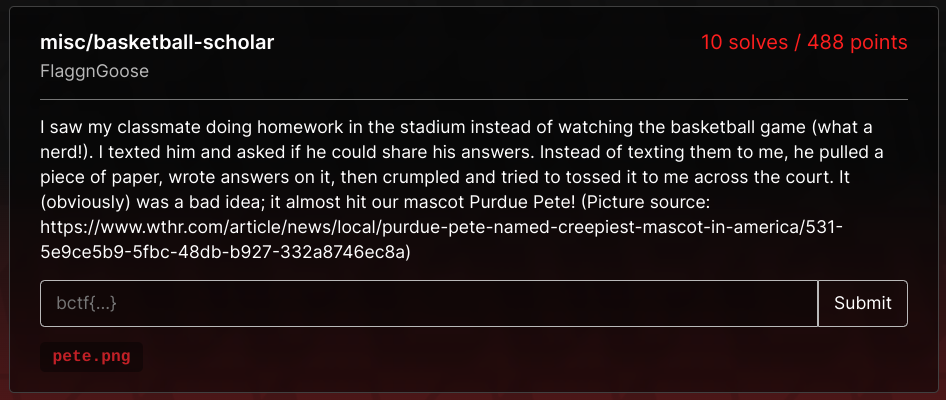
The pete.png picture looks like this:

Around the top-left corner of this picture, there is a sequence of pixels that do not seem 'natural' in the sense that they do not 'blend in' with the pixels adjacent to them.
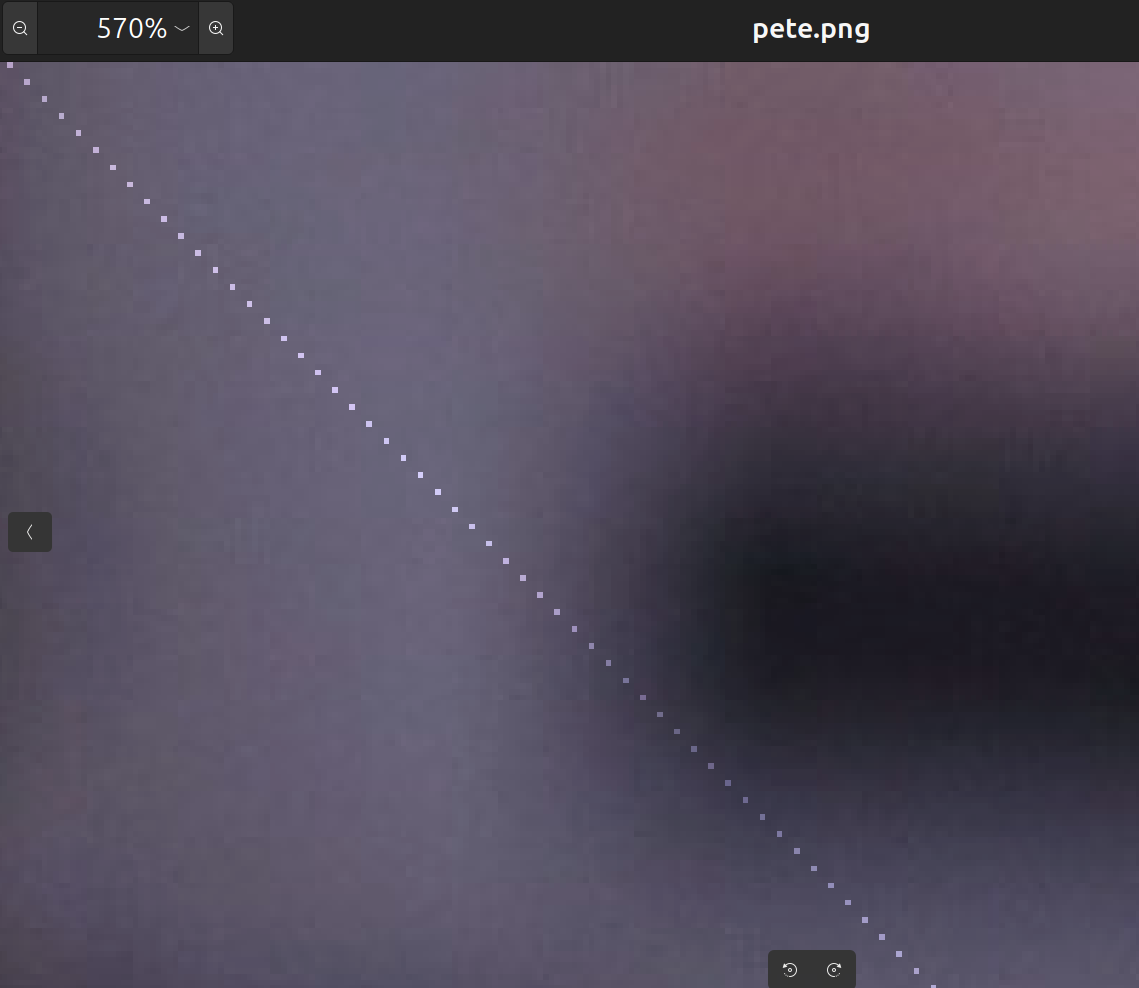
After magnifying it even more, one can see that they are like an 'arithmetic progression' in the sense that one pixel is three pixels down and three pixels right from the previous pixel.

(I don't know why every pixel in this picture is in a different shape. I guess it is just my computer being weird.)
One can notice that plugging this picture into common stego tools such as StegSolve does not give any meaningful outputs directly towards the answer. However, cloacked-pixel generates this LSB plot:
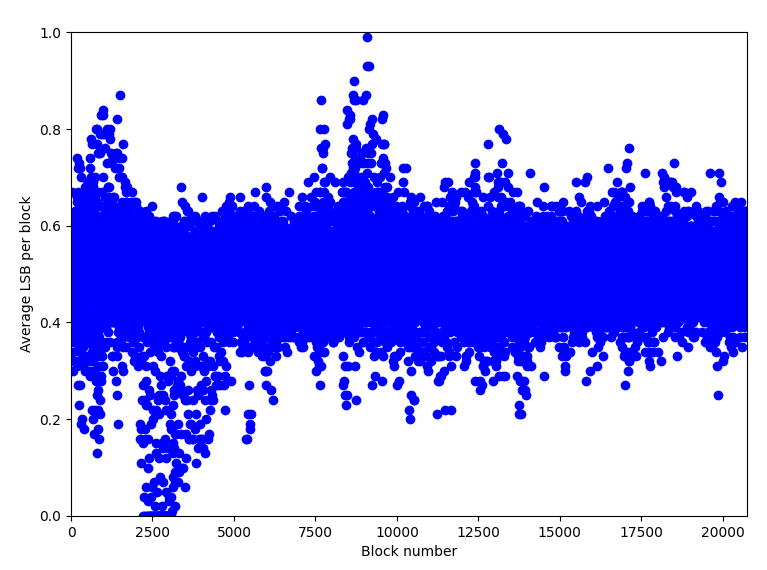
which gives a pretty strong evidence that this is an instance of LSB steganography. So, we can use the lsb function in the stegano package in Python to extract the string.
import os
import numpy as np
from stegano import lsb
from PIL import Image
import random
import math
import base64
"""
Code mostly taken from this Medium post:
https://medium.com/swlh/lsb-image-steganography-using-python-2bbbee2c69a2
"""
# -----------------------------------------------------------
def Decode(src):
img = Image.open(src, 'r')
width, height = img.size
array = np.array(list(img.getdata()))
total_pixels = array.size // len(img.mode)
hidden_bits = ""
index = 0
p = 2
while p < total_pixels:
for q in range(0, 3):
hidden_bits += (bin(array[p][q])[2:][-1])
index += 3
p = index * width + (index + 2)
hidden_bits = [hidden_bits[i:i + 8] for i in range(0, len(hidden_bits), 8)]
message = ""
for i in range(len(hidden_bits)):
message += chr(int(hidden_bits[i], 2))
return message
# -------------------------------------------------------
if __name__ == "__main__":
cwd = os.getcwd()
path = cwd + '/' + 'pete.png'
decoded = Decode(path)
print(decoded)
# b'VGhpcyBIVyB3YXMgdG9vIGVhc3kgYmN0ZntHb19iMDFsZXJDVEZtYWtlcnMhfQ==\n'�èÿLÀB��Ùßõ?��äAnd VGhpcyBIVyB3YXMgdG9vIGVhc3kgYmN0ZntHb19iMDFsZXJDVEZtYWtlcnMhfQ== at the end is This HW was too easy bctf{Go_b01lerCTFmakers!} in base64.
Flag: bctf{Go_b01lerCTFmakers!}
During the CTF, we received a few comments that this challenge looked very guessy in the beginning, but at the end it was created very logically and actually not guessy at all. I will call this a win.
TeXnically…
Apparently I cannot copy-paste the server-dist.py code directly here. Please click this link server-dist.py instead.
Though, the only crucial part on the server-dist.py file is this line:
\newif\iflongThe challenge description says "you can program with LaTeX!" and this line fits its vibe. This is how you define a Boolean variable in LaTeX.
Anyway, let us try playing around with the server. Netcat into the server and type some random string like \texttt{b01ler up!} as suggested, we get this response:
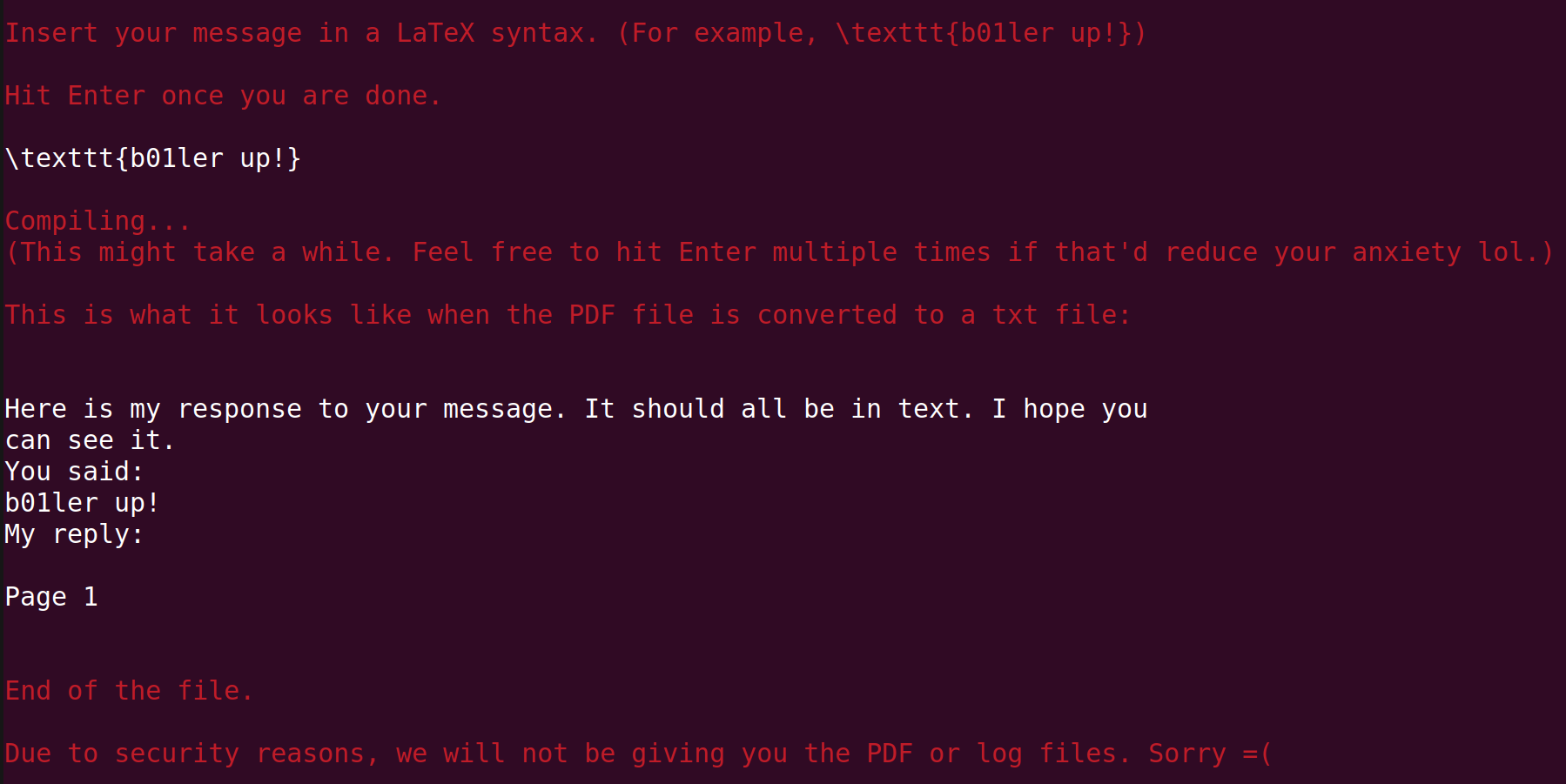
So, it looks like the server first complies the .tex file into a .pdf file, and scans and prints the strings on the .pdf file by converting it into a .txt file.
However, we are not able to see the reply from the server ("My reply:" is empty). Let us try disabling/enabling the Boolean variable we found above.
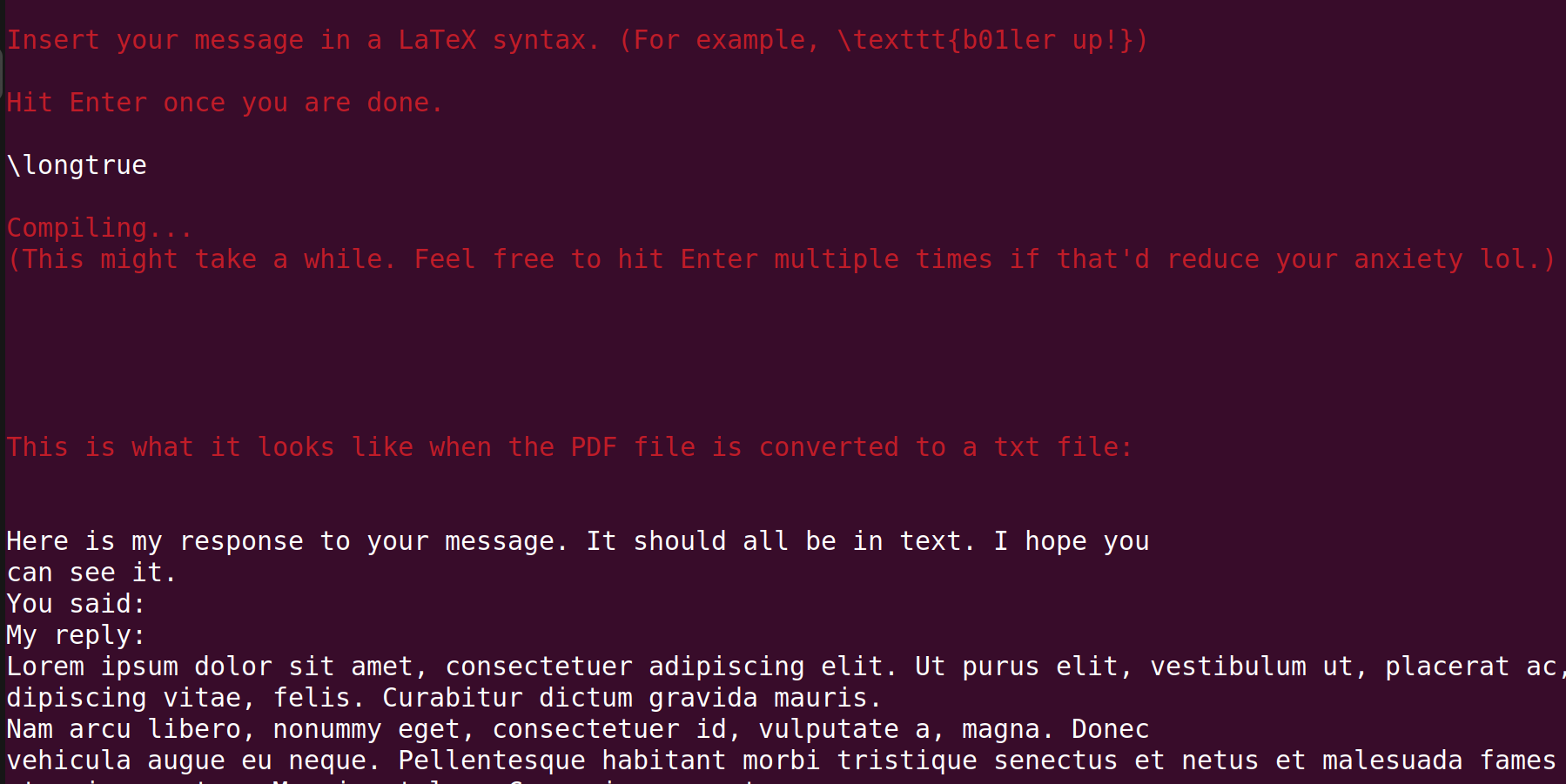
We got something this time! This is a bunch of Lorem Ipsums, but near the end of the reply, we see this:
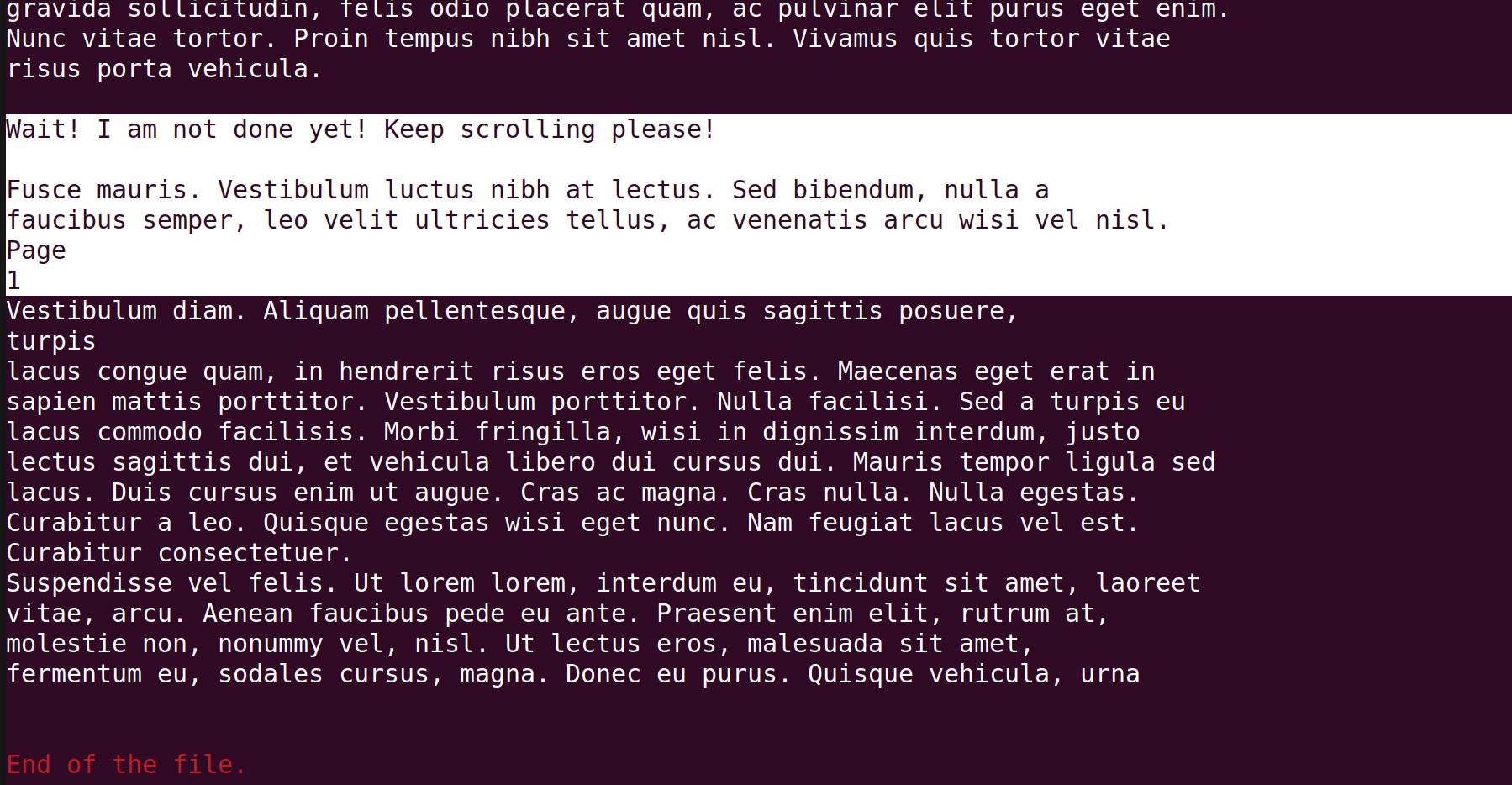
So it looks like the reply is longer than one page, as Page 1 indicates. Then normally, we'd expect Page 2 to appear as well because it is going over one page, but Page 2 is not there! This gives a hypothesis that the PDF file is just one page, and the rest of the content is going over the bottom margin. So we can try "pulling" it upward by using \vspace{}
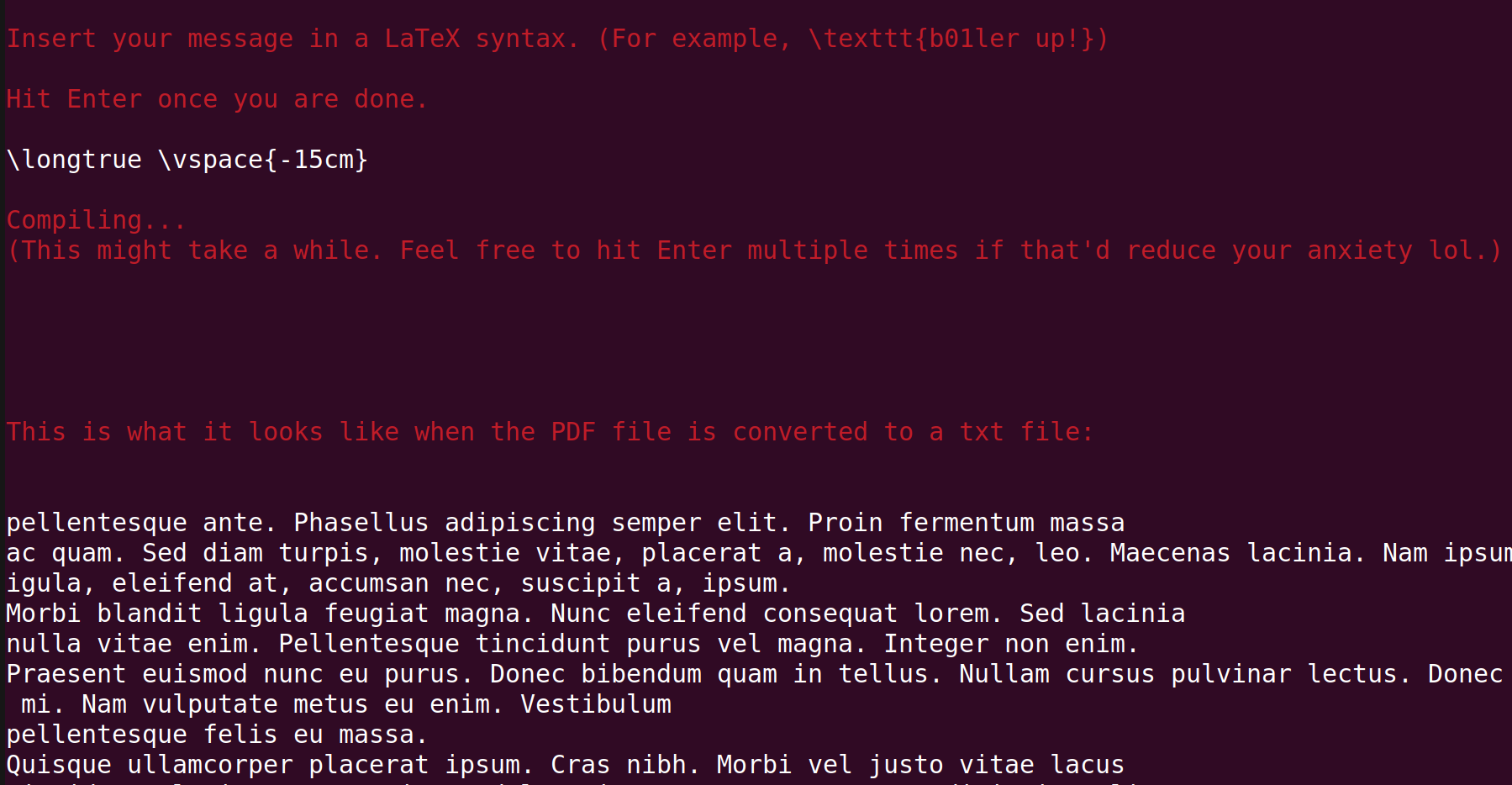
After scrolling down a bit, we get something important:
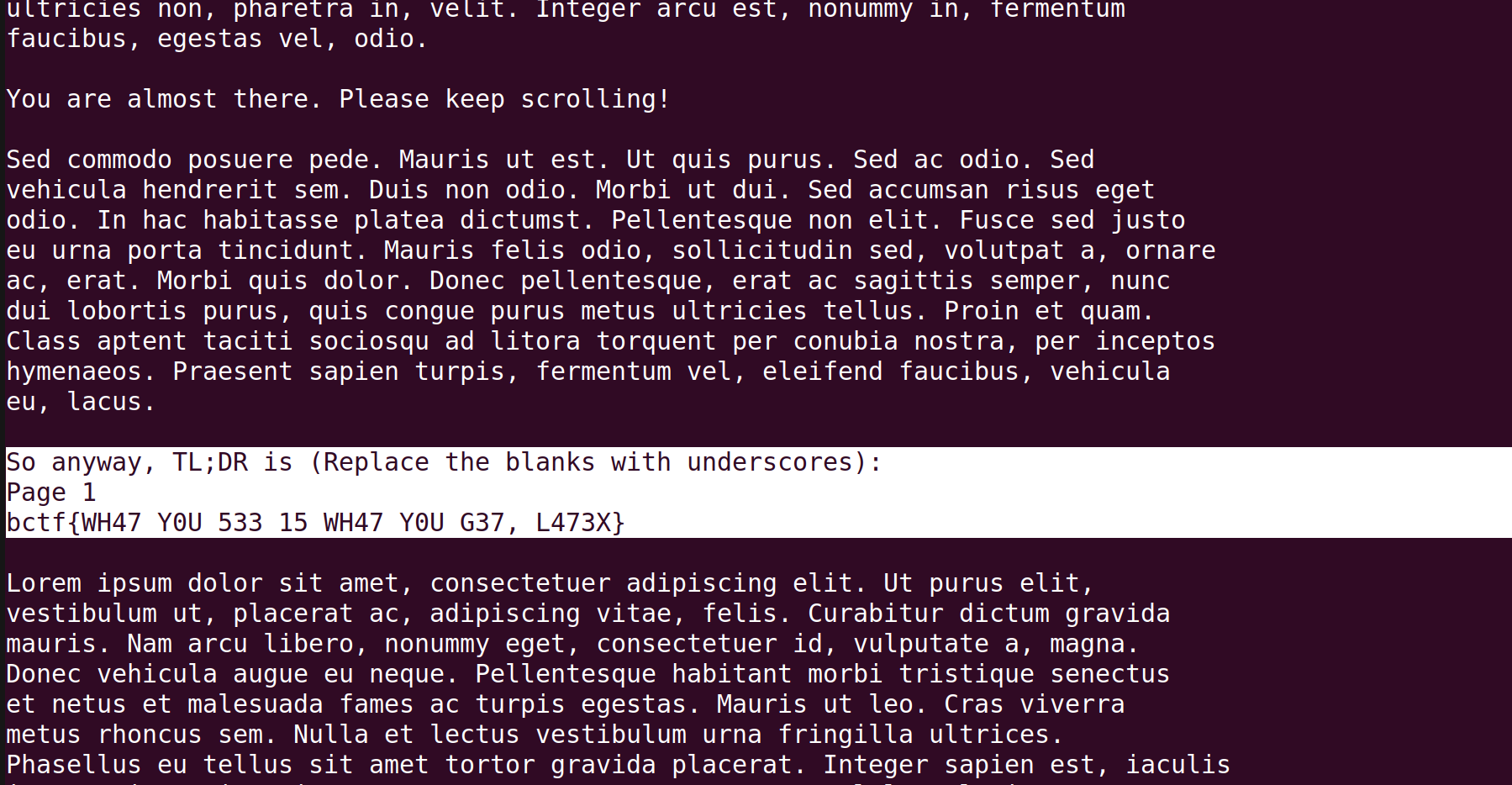
Voila.
Flag: bctf{WH47_Y0U_533_15_WH47_Y0U_G37,_L473X}
As expected, there were many different solutions to this challenge. There was one by Rev4184 who used the fact that the commands can be redefined with renewcommand{}
\longtrue \renewcommand{\lipsum}[1][]{}This line basically 'supresses' the command \lipsum by having it return nothing upon being called.
The solution by Elius and firekern is perhaps the shortest yet most beautiful.
\catcode `l=5This command basically converts all character l's in the file into EOL.

This was quite mindblowing. I would have never thought of this solution.
This challenge unsurprisingly was marked as the least favorite challenge by a handful number of teams. It required some trial-and-errors, which was annoying, but to make it even worse, the server was very unstable and slow. Hitting Enter multiple times allegedly was a requirement to make the server responsive and print the output at all. This of course wasn't something that I intended.
Hilariously enough, this challenge was down for four hours, because one of the teams unintentionally RCE/ACE attacked the server. In particular, they somehow managed to inject a code os.system('ls') into subprocess.py file. This broke the server, and made everyone who connects to the server get directory listing.
There were largely two issues with the server files largely. The first one was that pdflatex should not have had permission to run commands other than compiling the .tex file that it is given. This can be done by adding --no-shell-escape flare at the end.
subprocess.run(["pdflatex", "--no-shell-escape", "chal.tex"],
stdout=subprocess.DEVNULL)Another issue was that the server was creating and compiling the .tex file in the same (home) directory. This could potentially conflict if multiple users are interacting with the server simultaneously. This was fixed using the tempfile package in Python.
import tempfile
tf = tempfile.TemporaryDirectory()
with open(tf.name+"/chal.tex", "w") as tex_file:
tex_file.write(rf"""
...
...
subprocess.run(["pdflatex", "--no-shell-escape",
"-output-directory="+tf.name, tf.name+"/chal.tex"],
stdout=subprocess.DEVNULL)
...In summary, this challenge has taught me many lessons, and gave me a big reminder that security vulnerabilities often arise from lack of attention to details.
