TCP1P CTF 2023 Writeup

8 minute read

This was the first CTF competitions that I actively participated in, and also as a member of b01lers. I kept this writeup private for a while, because I wanted to use one of the challenges as a homework problem for the class I was TAing this semester (CS 426). Now that the semester is over, I can finally publish this writeup here!

The competition website seems no longer online, but fortunately I have all the challenges and my solutions saved.

Here is the link to the CTF website: https://ctf.tcp1p.com/, and the link to the CTFTime event page: https://ctftime.org/event/2001/.

Cherry Leak (Crypto)

from Crypto.Util.number import getPrime, bytes_to_long

p = getPrime(1024)
q = getPrime(512)
n = p * q
e = 65537

FLAG = b"TCP1P{???????????????????????????????????????}"

lock = False
while True:
    print("1. Get new prime")
    print("2. Get leak")
    print("3. Get flag")
    print("4. Exit")
    print("> ", end="")
    try:
        choice = int(input())
    except:
        break
    if choice == 1:
        if lock:
            print("You can't do that anymore!")
            continue
        print("which prime? (p/q)")
        print("> ", end="")
        prime = input()
        if prime == "p":
            p = getPrime(1024)
        elif prime == "q":
            q = getPrime(512)
        else:
            print("What?")
            continue
        n = p * q
        lock = True
    elif choice == 2:
        print("choose leak p ? q (+-*/%)")
        print("> ", end="")
        leak = input()
        if leak == "+":
            print(f"p + q = {pow(p + q, e, n)}") # nuh uh
        elif leak == "-":
            print(f"{p - q = }")
        elif leak == "*":
            print(f"p * q = {pow(p * q, e, n)}") # nuh uh
        elif leak == "/":
            print(f"p // q = {pow(p // q, e, n)}") # nuh uh
        elif leak == "%":
            print(f"{p % q = }")
        else:
            print("What?")
    elif choice == 3:
        print(f"c = {pow(bytes_to_long(FLAG), e, n)}")
        lock = True
    elif choice == 4:
        break
    else:
        print("What?")

The two main vulnerabilities here are: \( q \) is only 512 bits and the program reveals (too much) information about \( p \) and \( q \). Initially, I was trying to see if I can solve this by expanding \( (p+q)^e \), then play with it along with \( (pq)^e \) and \( (p / q)^e \). But in the end, they are all 'encrypted' and it might be difficult to figure out \( p \) and \( q \) directly from those without having to take the 65537th root of something. Then I noticed that the program does not 'encrypt' \( p-q \) and \( p \;\text{ mod } q \).

Let \( d = p-q \) and \( r = p \;\text{ mod } q \). Since \( p > q \) and \( 0 < r < q \), there exists an integer \( k \) such that \( p = qk + r \), or equivalently \( r = p - qk \). Then we can cancel \( p \) as follows: \[ d - r = (p - q) - (p - qk) = qk - q = q(k - 1) \] Being able to cancel \( p \) is a good sign, because \( p \) was a 1024-bit integer which is large enough to make our life hard, whereas \( q \) is only a 512-bit integer. So the first thing I did tried was see if I can factorize this directly, hoping that I was lucky and got a \( k-1 \) that is nice enough to factorize fast.

# d = p - q
d = 148453883883077309902302366488285249594229401805528869205703869056165014667369671408832746943116810089625561280030849110671983557813557299236174961479749301794264590800779357153051511218055095032342155018683815128362731175480834894355555440840342759234459037347799273558408552346372298731769329009889271289286
# r = p - qk (= p % q)
r = 8249003937440228449071189927841588166884296604522563914052645916882385936670872622271742736756321864091162906207999507013073663767227396402101199058596133

# d - r = qk - q = q(k - 1)
print("Factorizing...")
q_candidates = sp.primefactors(d-r)

Well, I was not lucky enough and this takes forever. This probably was as expected, because \( d \) is an 1024-bit integer which can be large enough for a laptop like mine.

Though this program is nice enough that it lets you re-generate one of the primes of your choice. We were able to cancel \( p \) anyway, so I can intentionally re-generate \( p \), cancel it again, and get another multiple of \( q \). Let \( p' \) be re-genereated \( p \). Then we do the math again: Let \( d' = p' - q \), \( r' = p' - qk' \) for some integer \( k' \), then \( d' - r' = q(k' - 1) \). This again is too large to factorize, but it is not large enough to run the extended Euclidean algorithm over and calculate the GCD. \[ \gcd(d - r, d' - r') = q \gcd(k - 1, k' - 1) \] This should be easier to factorize than \( q(k - 1) \) or \( q(k' - 1) \) for sure. It turns out I am just lucky enough here.

# d' = p' - q
d_prime = 147830585965696056210694302134044302026597758488273614447080150965390263584951228478674924841436264095688226131411349666321438210908975215784485934484703261540804861347506832527667072247145887831644874633925861762830560718182350065585805907874512596034013560571120754040750185687765406075698580816909652628498
# r' = p' - qk (= p' % q)
r_prime = 3207835794155802091423599620777434983360497864990442444407266396847764901780418857754307457498175729908283133570633340169983578506195299086076619940213424

# d' - r' = q(k' - 1)
# gcd(d-r, d'-r') = gcd(q(k-1), q(k'-1)) should be a multiple of q
q_maybe = math.gcd(d - r, d_prime - r_prime)
print(sp.isprime(q_maybe))

# > True

I somehow managed to get \( k \) and \( k' \) such that \( \gcd(k-1, k'-1) = 1 \). The q_maybe in the code above is hence the \( q \) that we were looking for! We are basically done here then, the rest follows from the typical textbook RSA algorithm.

p_maybe = d_prime + q_maybe # because d' = p' - q so p' = d'+q
N_maybe = p_maybe * q_maybe # n' = p'q
d_key = pow(65537, -1, (p_maybe-1) * (q_maybe - 1))

encrypted_flag = 1112756320743293514728604525847074125627733499921463333574874216864174267394861359286878300339098031725998274582068953774540185599464072598516315639630690460227146279883068171959669152725786492749134647675005560314158636266341872857691047135338156449079208724786185193166432203661686097427216817687125818982281560775238922543854018846102761064000694203176099481040321701527408255448177189569294847869263449653947164657780333770045806695817380760359635553454515270

m = pow(encrypted_flag, d_key, p_maybe * q_maybe)
print(long_to_bytes(m).decode())

# > TCP1P{in_life's_abundance_a_fragment_suffices}

Flag: TCP1P{in_life's_abundance_a_fragment_suffices}

Curious readers here might ask: will \( \gcd(k-1, k'-1) = 1 \) for all \( p \) and \( q \) in this problem? I have tested it a few more times and the answer obviously is no. But regardless, \( \gcd(k-1, k'-1) \) should be smaller than \( k-1 \) and \( k'-1 \), so \( q \gcd(k-1, k'-1) \) definitely should be easier to factorize than \( q(k-1) \) and \( q(k'-1) \). If you are that paranoid, you can factorize it (maybe break if it takes too long) and find the 512-bit prime number among its prime factors yourself. Something like this:

# q_maybe may or may not be prime
q_candidates = sp.primefactors(q_maybe) 

for alledged_q in q_candidates:
    # We know q is a 512-bit prime number
    if len(bin(alledged_q)) - 2 == 512: 
        q_maybe = alledged_q
        p_maybe = d_prime + q_maybe
        N_maybe = p_maybe * q_maybe

        d_key = pow(65537, -1, (p_maybe-1) * (q_maybe-1))

        m = pow(encrypted_flag, d_key, N_maybe)
        print(long_to_bytes(m).decode())

# > TCP1P{in_life's_abundance_a_fragment_suffices}

For the sake of completeness, here is the full solution script, for your reference:

sol.py (Click to expand)

from Crypto.Util.number import bytes_to_long, long_to_bytes
import sympy as sp
import math
# nc ctf.tcp1p.com 13339

# d = p - q
d = 148453883883077309902302366488285249594229401805528869205703869056165014667369671408832746943116810089625561280030849110671983557813557299236174961479749301794264590800779357153051511218055095032342155018683815128362731175480834894355555440840342759234459037347799273558408552346372298731769329009889271289286
# r = p - qk (= p % q)
r = 8249003937440228449071189927841588166884296604522563914052645916882385936670872622271742736756321864091162906207999507013073663767227396402101199058596133

# d - r = qk - q = q(k - 1)
# print("Factorizing...")
# q_candidates = sp.primefactors(d-r)

# d' = p' - q
d_prime = 147830585965696056210694302134044302026597758488273614447080150965390263584951228478674924841436264095688226131411349666321438210908975215784485934484703261540804861347506832527667072247145887831644874633925861762830560718182350065585805907874512596034013560571120754040750185687765406075698580816909652628498
# r' = p' - qk (= p' % q)
r_prime = 3207835794155802091423599620777434983360497864990442444407266396847764901780418857754307457498175729908283133570633340169983578506195299086076619940213424

# d' - r' = q(k' - 1)
# gcd(d-r, d'-r') = gcd(q(k-1), q(k'-1)) should be a multiple of q
q_maybe = math.gcd(d - r, d_prime - r_prime)
# print(sp.isprime(q_maybe))

encrypted_flag = 1112756320743293514728604525847074125627733499921463333574874216864174267394861359286878300339098031725998274582068953774540185599464072598516315639630690460227146279883068171959669152725786492749134647675005560314158636266341872857691047135338156449079208724786185193166432203661686097427216817687125818982281560775238922543854018846102761064000694203176099481040321701527408255448177189569294847869263449653947164657780333770045806695817380760359635553454515270

# q_maybe may or may not be prime
q_candidates = sp.primefactors(q_maybe) 

for alledged_q in q_candidates:
    # We know q is a 512-bit prime number
    if len(bin(alledged_q)) - 2 == 512: 
        q_maybe = alledged_q
        p_maybe = d_prime + q_maybe
        N_maybe = p_maybe * q_maybe

        d_key = pow(65537, -1, (p_maybe-1) * (q_maybe-1))

        m = pow(encrypted_flag, d_key, N_maybe)
        print(long_to_bytes(m).decode())

# Flag: TCP1P{in_life's_abundance_a_fragment_suffices}

brokenimg (Forensics)

This challenge was pretty cute. You are given a PDF file of a love letter: chall.pdf. You will soon realize that this letter is to sweet (?) for a CTF competition (I am obviously joking here, but hey, I'm sure you'd agree), something might have been hidden inside.

Upon checking its metadata (I just used cat chall.pdf on terminal), I found this inside the entry for the file description:

Maybe here : 150 164 164 160 163 72 57 57 146 151 154 145 163 56 144 157 170 142 151 156 56 147 147 57 157 63 126 144 162 115 160 164 56 160 156 147

This looks like an URL, given how the second and third numbers (164) are the same and eighth and ninth numbers (57) are the same (URLs start with https://). So I tried this.

from Crypto.Util.number import long_to_bytes

maybe_here = [150, 164, 164, 160, 163, 72, 57, 57, 146, 151, 154, 145, 163, 56, 144, 157, 170, 142, 151, 156, 56, 147, 147, 57, 157, 63, 126, 144, 162, 115, 160, 164, 56, 160, 156, 147]

str = ""
for i in maybe_here:
    str = str + long_to_bytes(i).decode()

# > UnicodeDecodeError: 'utf-8' codec can't decode byte 0x96 in position 0: invalid start byte

Well that wasn't very nice of him. Let's let that boy cook then.

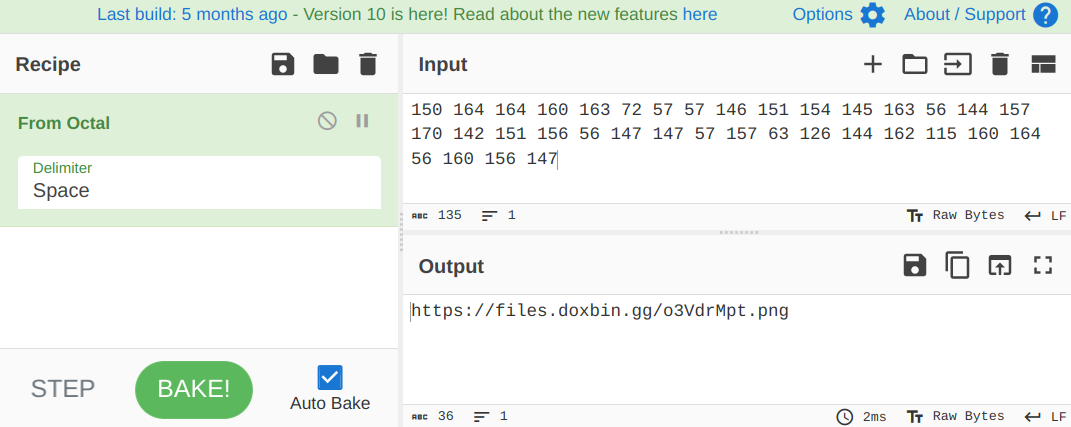
Thank you, chef.

Anyway, going into that link gives us this weird looking picture that appears to be tilted by someone intentionally for the purpose of obfuscation, or actually making people tilted (pun intended).

Fortunately, there is an online tool that skews pictures https://www.luxa.org/image/tcp1p_2023/skew. What a great world we live in today! Upon unskewing by skewing the skewed picture (pun intended a little bit), I got this:

Looks like one of those Wojak memes! After carefully transcribing the text below two Wojak characters (this can be more non-trivial than you think... xP)

KZCU4UKNKZ BDOY2H KJWVQMTHG
BSGUTTGJZDD SUKNK5HDAZC YJF5FQMSK ONSFQSTGJZDTK22 YPJLG6TKXLI YGMULPHU======

Given the number of equal signs that this string ends with, it was likely that this was encoded multiple times. So, let's just use CyberChef again.

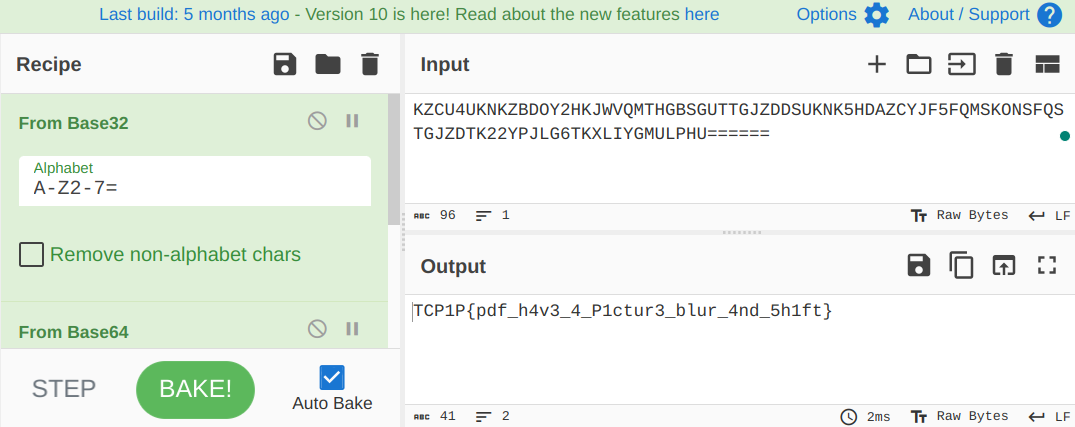
found the flag, as desired.

Flag: TCP1P{pdf_h4v3_4_P1ctur3_blur_4nd_5h1ft}

Jimmy Hwang

TCP1P CTF 2023 Writeup

Cherry Leak (Crypto)

brokenimg (Forensics)

You May Also Enjoy

DownUnderCTF 2024 Writeup (feat. OSINT)

UIUCTF 2024 Groups Writeup

Integers of the form $x^2+2y^2$

b01lersCTF 2024 Writeup