New Year CTF 2024 Writeups (RSA Party!)
Published:
b01lers did not play any CTF as a group over the winter break (we technically played one, but it was right before New Year's Eve, and so basically no one was active) until late January. I was looking for something that I could practice on my own, just as I did with UWSP CTF.
I found this CTF in sometime Jan 13th-ish. This apparently was a (few days less than) two-week-long event from Jan 3 to 14, and I happen to find it a day before the last day -- what a clutch.
This CTF had a myriad of challenges. What was most interesting to me was that half of the crypto chals were on RSA. So, yes, my goal was to solve all RSA-related chals, basically throwing an RSA party for myself. Long story short, I could not solve all of them before the deadline unfortunately because I got caught up with my research work, but I managed to solve them all later.
It looks like the CTF website is still alive. The description on its CTFTime page says this:
We plan to conduct CTF for almost two weeks - from January 3 to January 14). Due to the fact that the Republic of Belarus is located on the border of Western and Slavic civilization. For this reason, in Belarus there are 2 holidays called Christmas (December 25 and January 7). There are also 2 New Year holidays - January 1 and 13.
A CTF commemorating cultures and traditions? Yes please!
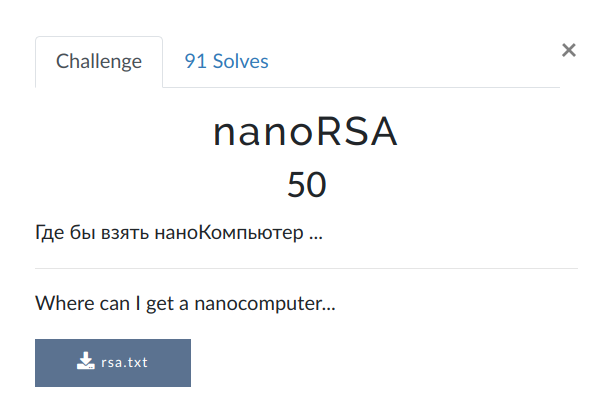
nanoRSA
## rsa.txt
e = 1
c = 9908255308151638808626355523286556242109836830117153917
n = 245841236512478852752909734912575581815967630033049838269083
As \(e = 1\), the \(c\) here actually is not a ciphertext but the plaintext itself.
## sol.py
from Crypto.Util.number import bytes_to_long, long_to_bytes
e = 1
c = 9908255308151638808626355523286556242109836830117153917
n = 245841236512478852752909734912575581815967630033049838269083
print(long_to_bytes(c))
## b'grodno{R3sTcD4gH6iJ0kL}'
Definitely the weirdest chal I have ever seen, haha.
Flag: grodno{R3sTcD4gH6iJ0kL}
As a programmer …
code_RSA.py (Click to expand)
from Crypto.Util.number import getPrime , bytes_to_long , GCD
import random
random.seed()
flag = b'grodno{fake_flag}'
KEY_SIZE = 512
RSA_E = 3
def gen_RSA_params(N, e):
while True:
p, q = getPrime(N), getPrime(N)
if GCD(e, (p - 1) * (q - 1)) == 1: break
n = p * q
check(p, q, n)
return (p, q, n)
def check(p, q, n):
a_ = random.randint(1, 100000)
b_ = random.randint(1, 100000)
c_ = random.randint(1, 100000)
d_ = random.randint(1, 100000)
s = pow_m(p, pow_m(q, a_, c_ * (p - 1) * (q - 1)), n)
t = pow_m(q, pow_m(p, b_, d_ * (p - 1) * (q - 1)), n)
result = s + t
print(f"s = {s}")
print(f"t = {t}")
print(f"result = {result}")
def pow_m(base, degree, module):
degree = bin(degree)[2:]
r = 1
for i in range(len(degree) - 1, -1, -1):
r = (r * base ** int(degree[i])) % module
base = (base ** 2) % module
return r
dp, q, n = gen_RSA_params(KEY_SIZE, RSA_E)
m = bytes_to_long(flag)
c = pow(m, RSA_E, n)
print(f"e = {RSA_E}")
print(f"n = {n}")
print(f"c = {c}")Here are two lines that are worth reading carefully:
s = pow_m(p, pow_m(q, a_, c_ * (p - 1) * (q - 1)), n)
t = pow_m(q, pow_m(p, b_, d_ * (p - 1) * (q - 1)), n)
Function pow_m may look new at first sight, but it is actually the same as pow function. The only thing it does differently is representing the power in base-2, but as we all know that should not make any difference because the number itself does not change.
def pow_m(base, degree, module):
degree = bin(degree)[2:]
r = 1
for i in range(len(degree) - 1, -1, -1):
r = (r * base ** int(degree[i])) % module
base = (base ** 2) % module
return r
So for example, pow_m(5,7,100) computes \(5^7 \text{ mod } 100\) but it converts the power $7$ into its binary representation $111_{(2)}$ within the function, and then computes $5^{111_{(2)}} \text{ mod } 100$.
Hence, $s$ and $t$ are:
\[\begin{align*} s & = p^{q^a \text{ mod } c\phi(n)} \mod n \\ t & = q^{p^b \text{ mod } d\phi(n)} \mod n \end{align*}\]Since $n = pq$, we have $s$ and $t$ are multiple of $p$ and $q$ respectively, because $$s = p^{(\cdots)} - k pq = p(\cdots)$$ for some integer $k$, and similarly for $t$ as well.
I don't know if this was intended, but I noticed that $s$ and $t$ are actually primes.
s = 9679603728276260450163332348967772341039656114836199341829623928424883179482998295442569610750090617263140422489655203690606051598227889033133696824561049
t = 7544882607176903318920087402887255144232202298941096774820758222068650540914461606464972583857391951228165370888600203959000417894282048977659598507065283
is_prime(s) # True
is_prime(t) # True
which suggests that $s = p$ and $t = q$. In fact, it turns out that $st = n$, so our claim is actually correct.
p_cand = s
q_cand = t
print(p_cand * q_cand == n) # True
So we are left with finding $d = e^{-1} \text{ mod } \phi(n)$, but such a $d$ apparently does not exist. But this is not a big deal. Since $e = 3$ is very small, we can just take the cube root of $c$.
phi_n = (p_cand - 1) * (q_cand - 1)
# This one doesn't work. d doesn't exist!
# d = e.inverse_mod(phi_n)
# m = pow(c, d, n)
# n doesn't seem very large, so let's just n-th root it.
m = c.nth_root(3)
print(long_to_bytes(int(m)))
# b'grodno{Sm4ll_e_1s_e4sy_t0_br3ak}'
Flag: grodno{Sm4ll_e_1s_e4sy_t0_br3ak}
For completeness, the full solution script is provided below:
sol.py (Click to expand)
## sol.py
from Crypto.Util.number import long_to_bytes
s = 9679603728276260450163332348967772341039656114836199341829623928424883179482998295442569610750090617263140422489655203690606051598227889033133696824561049
t = 7544882607176903318920087402887255144232202298941096774820758222068650540914461606464972583857391951228165370888600203959000417894282048977659598507065283
result = 17224486335453163769083419751855027485271858413777296116650382150493533720397459901907542194607482568491305793378255407649606469492509938010793295331626332
e = 3
n = 73031473813836265586802638898480963691823354032947424211844799982034059370278732061933096537003870674600636644919039367055380810706708777069353371137325457767601410808147577861559266484151023108122144110129865120907211821459436706652522768143661973946322182602994587756648586727110169581118048980551661961867
c = 102440249906188112653112850149004638920041731819150591992314684890766079962216378675563173361005618897820395598884602786493326797681447423552807411034991287447489220834908286512061803086201262036007513517016439047998253997542610533
# is_prime(s) # True
# is_prime(t) # True
p_cand = s
q_cand = t
print(p_cand * q_cand == n) # True
m = c.nth_root(3)
print(long_to_bytes(int(m)))
## b'grodno{Sm4ll_e_1s_e4sy_t0_br3ak}'Two Points Again
The output_badRSA1.txt file contains $N$, $e$, and $c$ as usual and He_chose_the_wrong_parameters_for_RSA.jpg file is some depressing-looking picture.
I honestly have no idea what it is supposed to be about because I managed to solve it without using that picture.
## sol.py
from Crypto.Util.number import bytes_to_long, long_to_bytes
N = 894011376132861406416081994144221048298348543110763436400156707035479762291337096368301340210777912166253392435275663746074998964323198306974285233167719096055553347615918699581765041856450618725024365550285245909593290693757548300976025136185960841538482656726074757217987326418213368306947431668797511869941369363510575799319146232381645606378509284692783439527001482275434870365007864755014763434476875230779298152747668036103797086099448952638933614839186234115539057353208089196503236476069765055958643599622359809306429773621018079928117609961649006558217734057147235098517323614637509521563090769478823258676357262436290835475545437211168106617010859479612214627871047960151415095910992231687737019157788664429412462674876326653667300420128914036327499885103193423178025962079282185227746880809451234195481664650147610375976243181422075319601793906090392759832052648670731266344219250793991957964535801285606036631861341696305110038590888086491568683507575846576623827059055577036404611548224528600604898405714747157240730264673180051312634408192644777331633111950232485559076080686217541095754245034143596485147084607615402187454830802772582891800608645679493263524678084504132604846410243911260803002065871918398725293311473
e = 49999
c = 127990258916322713210704002931365496210647826869578493680557063836772515914303363145985391647430839311330158084206710072455465957218072448099969815961814463831667357474852426061475210363277306704257877402661232669936031043625938011115290529377505573367883714424182150449678726041360949463375982144652910707759221795772350872426009873120527309342093683340576731241704191541296890578962805029558926492259701366885936092059693759354255247540815813052543086204934376066884066060405947003334121725632674642690548675916126384013014552545338699198239765357561083183401525044638243204528501965028598782513999767237563252331767079569128151380305983732341553403814650118788711703476805307790685184506737890913441497269132749881622937761764492015610811577966553776703680435092016590690563200951474073620866158140866931856293211794418637441400021472249887178225738960768608549559781531479910409684884180658879621882231073123533851227894797415625533435081416099549459198508358607887551022339960981663266529984544362524495679204397590064106335341279871204905873532415276380340515150499389237587052633736125460704219829657692767592459700685070039056607335118481257774532132073976558433243315868939654221066341581052013795470559435542389710686098062
# factordb says N is prime
d = e.inverse_mod(N-1)
m = pow(c, d, N)
print(long_to_bytes(int(m)))
## b'By harnessing the grodno{m@thematical_pr0perties_0f_l@rge_prime_numb3rs}, RSA provides a robust and efficient method for encrypting and decrypting information.'
Flag: grodno{m@thematical_pr0perties_0f_l@rge_prime_numb3rs}
39 Bob’s Friends
## 39_letters.py
from Crypto.Util.number import getPrime, bytes_to_long
flag = b'grodno{fake_flag}'
m = bytes_to_long(flag)
e = 39
n = [getPrime(1024) * getPrime(1024) for i in range(e)]
c = [pow(m, e, n[i]) for i in range(e)]
open("all_letters.txt", 'w').write(f"e = {e}\nc = {c}\nn = {n}")
The above code snippet is 39_letters.py, and all_letters.txt is the output of it. So, there are 39 ciphertexts of the same plaintext and encryption key but different modulus $n$.
Looks like Hastad Broadcast attack could work. Let us first make sure that $n$'s are all coprime.
for n1 in n:
for n2 in n:
if n1 == n2:
continue
else:
if gcd(n1, n2) != 1:
print("Not all are coprime!")
break
It looks like they all are -- good! Now using the Chinese Remainder Theorem (CRT), we can compute $c' \mod n_1 n_2 \cdots n_{39}$ such that
\[\begin{align*} c' & \equiv c_1 \quad (\text{mod } n_1) \\ c' & \equiv c_2 \quad (\text{mod } n_2) \\ & \vdots \\ c' & \equiv c_{39} \quad (\text{mod } n_{39}) \end{align*}\]And then, since $e = 39$ is pretty small, we can just have Sagemath compute the 39-th root and hope for the best. This is worth trying because we don't know the factors of $n_i$'s.
c_prime = crt(c, n)
m = c_prime.nth_root(e)
print(long_to_bytes(int(m)))
## b'grodno{I_s3nd_y0u_gr33t1ngs,_long-no5ed_b4rb@rian!}'
Flag: grodno{I_s3nd_y0u_gr33t1ngs,_long-no5ed_b4rb@rian!}
For completeness, the full solution script is provided below:
sol.py (Click to expand)
## sol.py
from Crypto.Util.number import getPrime, bytes_to_long, long_to_bytes
e = 39
c = [13452030216523953939619383306567156237847179958708487612576217529719746665222395820486500466482504139135719152618712682436188495760219709375670681309245754675625056568324297989848439807900099669843147994940769083142651064784002582187241241574390159858579187093445503830619987425799289118393084166589170167515536438552485957471749167975482212640450623622804089115884133484899554434378952468664363578732577799065562085710181775891100587254221033679206388597942893391949550285265824806852534919083216892542979179028670850849430881498411894714858013880685962108482870788197904595657359759234615206577093407963721091655476, 6647952240537339162297114431193478239549312701267530890821985753571212211642174014288542095599984264275979126279399352688565641573700777917652798103466392836517745766910577625132717593691664756145830000033528440695640956135077937254098327684533019850135332466540138937654480735713758056223861385937513232925937918233329143485600425620424763729210072956561549608623892192158548426500206774203018814452992272854859639224184391933347062144067243818281560846175433002236748580886627613168151665610107186058193818465259694217708476861373649508385324421227786053428982595084785245715507894275852348142288696426638888894130, 24223369275550586406762360800189496213101355968951497400728502448365159123810873003008771251811084121894458200596852602228386934066840026198948456908684885672602308360143661995013145867595220760966955955076217234184891877021819113945971859376116233587348653474621483002667718542867480532638393391491393669833632884755951520607320174066352633056525178479701744142373190604907050412026469040689825814279267745691274719991700439755812120961904504819754947863311288063598449308053628665190275387130321593024404398922509482124774012453772276609037351237674060267651705849713396738799960957293384215228052472200702241839852, 2245271234079735338756077429516219782161291729498951265748997272957386834645387003585524924986791019442046136429282850637635728471618779012311211284993914549619074958538639532710381561526587547326522287589987578528756233528132367252359293040702296101623756550326355333360084055314096631002209410185145417136061320174615436619439271454273225587096888941409930177915367460713910550173248108328650858953648584687533934013226835864412117007580133632362248311764963911739014177891703973051353137363907903968608612799031428830415922050970749112153040718172701931636803492720410597359282618038484148637828988500779280206998, 19344774267924862444124898781903069578455042782988343047702311526085518331897864858575402953670456148185935730586597845814345743897325575408930499026593721621389619005987807676110088961683563455230088363119205593316403686559928333602513519978735928368771651087147144738441819048989644499540361867664752683689745131701063534071138279747438851258445899085093951069251696463991476334166852751665466627954052069759293478776673373184820742583131364331845592152431762353201270001157439880439655597264940920942943676055189370825312739217807699413717893672453921115543172072648619733818406391160577906164114232350529778432189, 7842296075929851422401714493856703982996353737338134811598921100275080138097411085988789032887177193057478601313497256546467972688343316296527684974748279786281354132466718861963618248662832794950629338845837034217217451857012744269311748927888817831856257194392543689415055214748065934717038755857174443844562588648228008489079156963433288357417439812117107808612742943260191977571239375553076398934048368665427550076164026939953276966390662907531768494315615585400342882217335085767652173171984429912665644561734465072407032178183604166491811917422302200754609365656163364956530080515207166742356265956055906236413, 15523365660872875624859968571712078483925267513962743996763720394691533947961235962441850339297042159609241202494868455761546730986979032276186440672489463952133381414207611126167155355384874900630308726561231581992797954578395832110663758665116732737340401066967304796962331394644101924222355635940479979972726802340224733526756923697635287571358547276777227942683182249946166955023204990803416618834389627000684046735711894086751057535639297099157147938033483064172273077060226204974833512804567045308001461588389302980746672392230977680156534094086894599744166985495912934369429369837782638166866190193345528466046, 18404174431763998155513505499702030937609288446654518444507219180486190457622149224182040466809797922515533511218910563903155276413750794285686548736887473854998786343188790923412032246512390514994444307322917873129765101857216298497066167822291299636393153696075203572986036199430661446069063238991135447877201329970893780499329455173158085474209910091817150153235607824586304634817012532234934029690427153726453971060054569470314670774005002282574106570446904024556401239208701941567682691580581001397954083269279245932278728653572143196993304429174083732915608742205935725759773745092983506884615344937489713957319, 14826721267958585897347074682031124104677709981665283578114167372601038779720004173630676663448983220734652287932071315900228088633098746052113782637575433897839926051273163967069317276951346222895825474635957767800817883661666153431458505918822082428509580159702473481845761246880217287423849927796775311500290200016466974921932605776723816597966077251489066717304282958710334290715569084325703896393040613215757717913210497194995219364103661712575920724737080632988055454851873774016901037975282035741115061466945503938782140224412294287308756678093888590410840815840495794393014709080557041228538417290845039986629, 1725892619153788723565024992720496319035328243193511017386192659734565274087464015072271209372532880865643908857948259778304017741412587250679332505239517089295045888022248301982949335264954153878287933761031900207143533639611811961239050235477865529343208873224902393679707429894523508744632052925816505456495178716905292855898291100191525335064580854456973378866796922894276817167016625092966554139965582893976988929995479939058059525923075045237086011684854952911299052403086734214780504065029236480371713541508547874634034474220407595910284217614058511692102639225851042892925377443067854738811908145489828518614, 8058573350272932452787358937772243268232035683824730527587670438144829032503748299486907654705894478786415390404810104943133656866005402602783640491312742032603103556043796024557223758600317385085904802092687434505810083814171988342149805733459233212859665360022287927473071502135204176160854276321175696914236585023388105179076159635181204029497338035973372152662939550428747245966356552726612414901128417495410296863958667844783860062846524106176907323938811912833104931394019505443571927656505585752763980175829849191915479102259286876797169523610109895651700949804651084938132883817204522253861181317178024383284, 21694887419287863090250540212591797371653307577649283567710899126994776352971328966774555525851919386051835301112421639358519024960202947895344666007209123229462877048370142045763566916944619445334470440100618458005916180148607718682767853885401663244724776224552637243518349416983408253534786964558243227735476056785814458409540305876028970128943691558734925627925624079843912415919415803082621797620050955965213790705204889405170266450826089316599091255209600557374911673073452875477595527420530638513480756398660655381893057410546275912448934880072854513526588604902531550849926769131275144443280988681812589048101, 17481407307242350549545653759305086331639695993173803626151231774676067197599297096343763205782297650442262867279790489401262844023740923684917910571488842405376036983264848529361363225350117493584325189345805504048853824561861997291126344488107422737188838406700679694435824530633418899929030032532772209488257971967308792185014753986881854812772702859791565314883952935891378768633353453298425051875233669225417624213877359335400197156494363150154813743931227759408520880206860848048148310137107998672011962883153069991091009167765237704757373176737633283124607417968524339785640360646819697517425340599975702021086, 7685519239517535204555668021373255464026444129088835315214097274941539272041403313072801561177908220204141453417769596488422436007237855288894281136605596958965478763608862539780666655780842143478070943724791195929071471517241201062685688333385023639316159367902237490584926973515522540806181884688198535516914899792538903804451751699075599503272228191761236007906274272662942501758857687627931807948386724301090553168212517473130327046477001682682454928784187616525837542469470692368260367872990646270788961967665695739655241784397200933731190846365131829484708548197048526144356602708170151101827352938757728121924, 7153134896370482764179432001823513242012686278238473189211341325892860651216444193712608422022118029761503719411871226645458663424341516228811033825300264512032228194371462831067538044773767056069395933837060217333943680091074214505723813245388414558004793115145704437761739682454044628153366939978612362624025608933970584817294105429162598247214159717262867301743237607284814278061377674689302897174507084694597527974054927147566848352077579602688456138902074794127793518837372036732554669011698967467658857861387266876486357129751039269532261382100714183855844820969200363968166656291685284833244500736174935247405, 11237942261049068522592043962941891973033822162223094419584686217427545197208728586270834392458946951363277793242386975518602649114541261684130652518128471456940382799836390961537469693335034132973101150632805199028735621233065418591342478572270924558571838343569466421735912359239456786199382709940531671256747165760725568275201188298939189027222781729511538055850311229526194418570037208041062572842333266015188815962051247074293145913769018413314668084403751090174729626241196293507717168937618276137758602583295799540746334832136731461269943863970294128252755260145236285832260914206031640744270955982230393818819, 10326013758073949205828031673851398448908219565945421085614530702123015052233791900754349457319452693081806705532896147726341526196516746416651128016642185589323117182049510081377113522236563712752152706373040089515971300031732358891093201659305970855444711006562925015388588701263215945164276806080441922010510777591347232375225406591170140988725067210070932478105969733477766413866751430193495594191904383150253195958486291520822450878945502454482704856999693912354706304271685293426701855513606494941555376866290034766893849834926647268365690667646281314267883881140326525568966141114331364329968073589534212528879, 8963664679677806387460562716247447276570414962898469515952024893063014702218091331467190958793820486678600106342572020637486736684143438780630714171815098724503422900861093176999703456418633808181495822161088083284064424229602642228091724647741774440410618756512697791082317979527354145436555587323673371804334227889061989593977742804092147757538565630697743441139509552453028951994734064615730340119088517456667178192145949183518342339175629924133445650085233397050821110950859513936885409213496607869242751151821280400494052918443462086438080973425978109663815694353405027755578619282048208115978451746402855261198, 11943860097317391736812076958390491809590965573786521934780515248451104841738077235438344230925358280134000587438347979133526182210581525686825867215868115890974770881283342844801624605293539675083927134892180534566469838814679806482747597461646180732503733469928832537466854566921164664531337890120290319825948348382335155812605340568305861809047603699653856919431760185505365921314825229019782765276665781545519332104214524301787843495274497057416893655562323001443973548616414547699700138283858771771305599480799054209961960089844822924228638620767354904494413144033817074545296484172770089427234904837723826639888, 5427523676979488549918246598831651324157630112360459647884727997246114195508507947231342762737379465368209924702888610864926110878948501909362554730712521229816452689542499209631103240400493337623781396944502192074290409649205002812062854825117125691328923220735185450066891825599740255844303951192890849127236620758106995779358172666433864048600507470512781662731891126726825275301696768892283259760132655418418459098948477630116332754218623328434866679920459751293154610218022355325958042129011661016559328069883674078571526890519701298634078647961009264521139445240874546956848724693095929968724672308956716593077, 5353521177589257350296181959380942694733004584931181704454830608464241555330239874567703651044912311938576743556781859740694535683533668357688498101196308167441678291197304826703211604921076862803803444453998733748406353530339278748501523236578317896674870907087459984882214243007371024401856341872588255518325934152646142678961204846985589807871278982328962806931858846855670259138337162278219199099235302426201201851302945853115181170459199400836674056964856855183553882079629252053861069271648960607407369102405951798670332170706973789662001605549090154861131237191989485331119402754459787732651200040894999961910, 8650217921207076858208171985986295878306209967843017288579753308368993863458949967323232402996646051111667262112380515569837858408995738802005941894759444327061324229594308568926497769610515296067057304674769843533912940885562571966841385110361806983854997577584175940048061740241048775252813268520837236271126053301540926116136467193213726805609041132780663736805836848050597354706963793717827325373235009648019159875282387416593145402613178443082224062592435483852112361299020771749745693491331568760547531329729781834531746777394899609024535022880244238403925174664353139202653367150137872063761433559376852218543, 12452855613082180109580112078860570193168669711002372679761345109423341019392619843781283122822177959528230972757732445662482071923287109844326018594506728778735379485490129634234898491575228990773307579677927012543762945345593525272595294844247677267549735394457447094768180836699528029519051344173232615867246895791419873256898523473553086672249508890296686462445459394738988981923447701166335920121432425017964293757899637052849283540336592028986648069779579760314777920823894002271363251515635680867643763932923518000441731794925456528913023466116512255611572516776306064702177348207983423273653971611177128653270, 11123397846454771163301284412545495562739410727969572999148205653379090307636334302620534971989547648396890168634573238116152196360138732485946510737450974652305119455662325254254712176676195522919049246530863581876182176257530117111193315359791286852824507034279175866919044490255649323875532384872476513065597635943339969031707197334611955253657370831220845930143941994437970458939576704004975325645752802337162345512027614362199754170177001395231144427325331867626278551769726442969221312671968430022694270221055944353909293176513469963709161258730815414104459631395987239109281952751150058016969310942090743063992, 4076048019609087474679598433435166095517344123571620612279686316039540714577056574599995405215985442565449514627216002324582907712155987323598246214977286715337244943667241457006133665131444315546840172891838465234509338934498650271815986713237091560926127882604503699646773842325883767758907336249704506454979898102713813767633740555086703198098688265325767395166022998092330604171810056863294435869976133230435711997336810920495203446467907438446592325314748593791667014824369186424701569548849329546889576984961888854586610430543604966474737796017853292999190426258865594687649626020789242511871039473134945304077, 8298866160559983519286524313569166939918645401289815957328459020754211324675432742598484584057030993244491037425420045063169577476381116781031538843870724190103542723153580081009407312273267923235261348493760291428006943583283272431108462471479131626481110564814106590283679945306869113307678630540370494773839556748090037175760433328485890173258887065322915578424770687134656711370092290050414889018209300446920731282995183879796125608946337490054556321109294612158860161071975816594696747519839733977789041074734519699037205699786569671163834691336915157658453976152089886141211017767357335312971178612788506360860, 8790362698031085114443440199791620326350401827988997735372612339360395641356783442338059181200575988976848756000307462270594079399384593043570568485858492024579485244551886007674604031199724376138873950201321003678126838807045370219200333750789065058958853450060551024353361260536615483286114542838068018647185948819465557563023361446959148960106386282969990006107338163024306013321956108738790016852460010068746230931321286706050184754880123443982652441164325660385427850289204782705374421913082917161009895715101787213309938004768274833569845192251361422797256364207032034445772813789815643555853565932519462283870, 14820333991752712569715936018984677644994800427421552496592927607541659105847709465520945446887025125824730836774269723249992586915573737659957620112087648525065593883436745061856833476106300557721619770593455597849024500053720293125561400131116534992672463514775560933405988170878841273809755356643346836289364328962298084567895015076147866506305783326853272457955822973533031197729510215845091166120221963035630301930161374461284140073666246194031800048793440705713391767180704444689569153013985460564768806493346845840069423455091734261567163746786628680909869698833317264587518921531544540794855413725366011792420, 4036749847011727477767857719271784664924987177996956234163850231744414464918371522086867203769456400996655022995714777273380812888616698591837500429956560792912836027334837010047045463823794613501780388478699330622852243903002209401049370324001921532153779356900908839745563255732283694478556311458461651983797194786118285124420260130919929827386331315514499370170456609707999372650555240463002982220832976043420825400487372254976751111569042637382963856442792658454333656397458784837390570744294038728786698644617133747974128955997240719471221515540371255892748749987232724845485563516687661730012212878456936795682, 4600918187223439723281803701631118644178059157226665836080281633424211740545322480387016362764537857670949334356719051829613042300698051175425780991268981848862203103953184599245307916987116922985902111784422964384583906486285183742403555633653849337785433082153888293445513460969393840488006985293007426644454413515462692849339789567770116145722507860862447225562841391791164345610814134780828837555374627118579259926150896147824576728137051659624960053895130452778844804402133230439387713983241751567607025167813013557126556929316950982050630019478396288794990549923056750246631076045219940053339282987296723372996, 5059741277677133728954255119939605648006535233470553464305677466711626910956286913088251623264145406447500802240726642426969953609725602786086771230940854190602731104966435299062215339474307497542866524713537107450482487882524401408430440474976031445130935347704261908586174521263746583086200156082137884139435699117398180968196318098477371369419862622139819187732754646950580734123572542269239884383747585593408957292456885382728951645280542390567736842244101171030069854066960039512007718680452386291687884766422687060181407827489883305321818995670045365485790405737177937538196021088799917197746454274424946665818, 5767186853197675104631087493739746248655716404687246733068051121611996522228069866769196111111163525698584911666823470089683165266622673538822746885610156042091559991677925823199177025473408573918781127587569135856697309401925677388564862416012444273635564674283008155943669384541379310856745888059089347587146834028640929228350080647835222656215041410709633772669191824434747772661228799274792935246283791353611445419800719321619472546810653267253167789621578957283405424117425111012541346939820161708939218882007551868725968930886643674740547009618705218099626008628823773604342428215318901118234090036045375140689, 1352672224230808993249944798391533118330678391690894610169545197455799184002950805998331921432205767594064637604566225945734928687026686480892710473112638737393795064541877332415996481271367078981073598777816267932241085462081117879710041871415003198737526280984957935236060736302581093226686105864035676284644570665105237393367623096707659087705611798562387327301169864282111982604995854351330937610293708889561646104688461527173306437185436144762476834700245166113207214708005735658311143251405009317114408365330584164720447112314273001907261784830723587385023027150335608849908556887359824136327308170854579977267, 16448586988581045956359719078815777183802598248079723733813433052508270150082945395768172860357785068007369308113433653887136199737276591543693323379541364506206806311572118786005063186095101079421515265048396820325735728461134806334920041911450411806886297836713855239731622958641773801673142846113863846326649582601935637747941323982628654409906182277644278003415837452451597207786266418100670981859953398195054712253071295161358928644463220358463012394780994485016224920395567380142168883515567498301374991455117371465300675273827851155323753964782287200328343947816492699107268290637155181874142073850660420608413, 766228197824044112159114871374332322553770815012186881678900181220405338965576557681718047808325043350613094949423154797278708917185065414564349879122210933092074806427791777569540928050744210842939317144815596684069860466743247363602206676912072534344704471461193654722957342321106287196543283584302456305053274569142642591209946485707759693424240837434920728093029195286778445010648889662853011487456830288341512796018606154668243724011962935147804923699641549386720944244859140341929547431504405158762503006182260323008256725565454736832549433597971962981887887466986479534726856235822360979074080638040431524595, 3129117634295671130183100037934653657132259824630826877539310915172082221296896409731231323875429141628560251955276674605570457331780774540722132954632401513455749053982172082223213273256630551177292088579910320536117320359983189514223465935505425449260556150940075740837004834305275130533922810085756787703039517743071353641140395791657606031039845495171441476273534293590341424315558890584806428447170480706628332233674813221964369686965801748289175999234929846689685245745033661108792907015325264645178385308578177764222662137280693256472892280703647176377285280672349229535150666371961421998391645310327866863354, 15948610902280668891761614278114939164694050871119032907464909686242465635511078451452383908577754270091348275911138949825757018907690058499020936754924073289125454627530105940371351991824057881262563954459711857342447034025517567168808077012067699547151744182051834093334304507886353520826737058873924477608694762405938009732249537430126069175333508661591931291693486260491829927053477504223178798414428467346468116282470140986950484872566555028480321626441484809415258961941652859308901600074939485967993961400275132735932611655896150431542696289014634176552045033674844078602452955345996681899546393801774709623767, 2387206876487560328480427254844843159307210159556506481868980750760508814462646702225442052039244689372707130689213248663004238772139756810218704998437589203620634030076473238113722643194177883045114339115833732546231489811740832250160440074049583888196538775666503621652292945593213866420857126764457322887295759040654047246760116362497023238589434497823298704148971652984836945922213702452572104366247954379239559863777789838273759855969613359158326838803313462523556345260584656933690504930724625614408250630913989882111031919114538621990226554136060234785333036799663782806208712256551801573242530538347865094863, 15300107719249883651419959581182719638221237717254571958772653209683913102397091196694151514128198784163114148569358486374276415962710441860800559260280049209142842429459826683113455165855885816622035733822807838774819360698883312302394379245516135398863637243839155769029600296808022194972425909749769478016264559107683802749267175601765799027336834597276628928445716524027919100164029499509031356772177014279003446940633375795590627848537718285820047796367671823505776851409776614511841321593674011217528773597477914187554787313629681407659353182880040781830535548068735074638357852915193986621003364692927778385241]
n = [15643688268273884918944030648467072439980655704010303062646246065591858653229695482388076257132310837437692053368364731819503204355693172343726691658198352052317997442221755002290027935886025969305303876847976979783851684512029269169835458714118203309838485685465017934300251464374402267255789152637635610015145489716847503308409866386540904236761410219013756414792941254342787667876628869321417943039463992540229902772421578488939162804777083949330682111119547206886313353739274766184039362365746327921452933459051630625290531864848914879828719090817221421501728774000802810472703411793468023654800698876090764290523, 12819565797635549170123046005576120919320997757486568299698128294722076011891321537847604153195323927169286228257124997991409773920250689406368017909006012233548250202095043890966643271629028539825362220905562619029126187129733074150182591024018803125579108085625875228860001981587325272594540073450623063838585029245361939747722339766494680776710854718229506125494099981161428107730022247665127342130902244518248111786918846655090363553186062893008761601704801306956138696285000225503750254726650046810627028999205651845563780643724193839065810852398299816390412485730407189641077146231517992240371092408427305068941, 25117261747358142302904253361548173223891584569699193465130199466336086264058930883329757567869135306669440978402558122775257476632093898059983114570019595860202495496481304772554582115153427131331660655097439665099321031908010919948592429332088595797726370797630932366260552368890657825518745942662235224461568635833582687656280203244349104730602299251198700243316394032886693492860026513878161681981108991785154936309448324809354925554672936368655189447297581744995041403438225002146444357249679954106508877647116921016547399519497916961089527075045626282014025554687455596293236909271633913785473388920898946447671, 29447282901626145462818197353784841836443768464994822625801012119627859937220706877434686130766936212863301543642110723981611278128092709740933686802975794081825995144812572659367064260462712130524579270083497322132038157662741894765508049477642637178643736631552864396774175518676761781992229565194505666647741490308910335811411594148344650578769340113399069641661567868908267117651734083092863404502940816072783139257249071724065248969301154617034146904338257786421229227680878479003244636160120854948598784326295593051064645197534345293917693692415855751445583816325835009830139604166147980010612889177910772123369, 24066550522800184601744423870012281722828099284201665093241131424425638012618730346682707634081048857523333575520123244134622026823055794729163247111747009907511240606263588479328327086666964229516321705274443189216316166433957944344902813843138203420991947663331213532385058086636669408653718772260337168078523316328098171236053399011802808038069245845243295641613669423949517711637115127526208661711763710627861777870749857585682994564573190533808790761802415769285213595719616275692933159582542867449766674213144804081075751801547457259953333965881658277465769386929043177788283984828849880812154894357079570603163, 11429654911939272560619284530933908840296008251933138955655726835944140652955353241981690574131269516699161912883567556114644286404403671246540312191148824891851740604536860669644244585435878383803894446677404167710916425040735831817156190830340333711470253195091808009143665940461060721278952096771291996368000772174330399779345934192084574046750307881392816461871036435236880044071772374989103118881437897720473724230325444895366453783297391343785360369474232832810271850428851287428905319764370368432553225597440138219454415251699986249224901761399145210913847041568167543273629775611585198777240003935780771924331, 22684986728558040011420462975257973025858148749742859110894568248871018271393091701318947476785971451541136854373327939791199740063632717707982697814884384361712193493524779120767298035927299620564575352808896628417916312776208332961178550773608265507629139425586486964636464763938775962182159049925783758844080911305057745822499635536868796555245691686934221543277463306579142161495446071414281744866913515005134645661363949166770858345488031134180388640413709035770310755508092242434866170442881963340626859285584533537587563195682791964221126140466870297164887194315283373531295837290077614008548404277352410129659, 21887106116246293046422581449824552973504562183375327877274153883329134850009608094571994906431069113097822661597887880551019928504755092352276949203283374066616877536545758134454305014053915121618617368257391008922873634607832573764840138432388120683900223615293985759818476955823196861787763867198780505758279028425239110049886795179208180138202802914838171520350852147159994341297500596926555609805229551557841228601592637456405063490458889349850455760952588582431734969623880998747292981708963396918074542719009221616482276531802661287368364302071314381377475330496091506176369953500343787417728419095491873809323, 16190390755271537005708149130655236816731551827096899715422408406186693600060519044218224552214166621054861678271154517411160570984170929782651164435014780370293144425254292912389752188955752955122572296414519374962992948365097588190600245706044589204323240082079056401695986066047899543298927687811147819604935502036590980005572348199828163868995175052118280808143871700380402881375584428520168215706254699272028541717324002095727572379017841582648480236710307640949047363260103657981828092154438358593888981366553177132218600225956833488884002055379385410895652638076549578343084392672117880937996939715691147407153, 10245046862037686720731895584827011364496905230875027577573991408717143275840739718784022113693071463815254229843844495525965488476117528553821191672055739894510697952895361871075533166514214726153812458206982025289490335619718146967441737971504826482350041194579830116864731931850155048285027487198193323991661447416563031891319206336701694656896838572577240872796026333779292346848773430952714291592314361470406966816662082412136474373061114335970450961567475523046206899356236417397620263319244907933185908398591668823042569189887559459085872965361795124635053810929449172304754074768037779896605427583595291365121, 22043729620664640036916166080884163808388841523393860151133448204175802774602741743429265566174442992573217939244541096229786248367023809980138943022606489400838075998250741282465092079880818790456743481275251995109748201471317003383414820296898092861386061149732689940072951616050767391660547907684047165452699192508362811472773372328766246229881068257334041440537722984822321239259556709977611371960918340111896895060404733334443439418453982988645327534541331292921052646169372242653341542401636265904255168023835181996942795789740467461230844557925035700885587004228940871071878893852312301744208913597692246679127, 22635049877945156267559516807683669795545953699867669769027999408453015128839608406021372797988990940640118019726429280872047113876002943763544273829809696322657722905221995480426155882032855059000696485159508685794492083402385749899503419869956330364147589181531805116065101883182569748966237630908567921905267980507048636598432914006439586248613590222894463983949523823560024055539071758013159420392962553793657641068234832253859825800606699788375789965363197918490356197437007033262696220520859038849700758594563442634476068034297849558768504032571043539394968743343981913683299893988194877526769753576831498266699, 17546249610666687755157266202998474165736330891102242975713508541286945556395038217014895802999725482392950818793476146319033094019480292451617732085532823303930130372530680390355986961725256081314744516754523119423764646242640314272926192827260108814842195519276876029067117663070623260233513413545828103670769290815689835514629671149099923953016974305736867572982837343777767245677483472790746136353627188588655238152631729627477990911818502700014147664884144642845254376445183643796703473121133949002641048039853654720476344853873653697936689364899525502843245629305468702023968311705537984112577570223674389858749, 15824583100712374337833962761225930217670587548263430362166739824901691219508529353703168058003991430885630584064109622558304829945903736440549392743579755303673404099696231479581138995055358258181821910059033090367928980238651769540275689017115566985837859379465559732084116830242561809570285532979962101504551788071192227733808863905492475130935647865459913889220648078775968357935456252566628978200481610576595579612635215165417933057415114203106905001546187414501634402004201165676329172260284697855277690958511834616710599298907255783622325684035919788375044587185369389620463046243524337818137664476739564560001, 16927976473794338239130485938434036128537455981956905473825558285497918347115832923005810121350277247736540643720965148702347443909580236880961664537218799723498408289245463397006715590440844378247112926156323152493169764220053875606702742649357720243625449576272984767165452759028135067692867176150907322785586746238453651559415774389434552258081326825706167522756902560405883420302896081401825419083616083286832848652897207140500410240737185346821279713889828849121808384492319175846504315762866303882800609051188698559650465407480396103308594666430000794676647522755599762417476852364023719231737290098986305011269, 28814156396802300816419271365023329344891313402241999632770140904033068294531306564875148686997858286785268033685899015622106977000883448765982797117669681493066411472359719098886020510962234602630904747166084229222561243051957290031756712567556003741896355521451595834548686543319754297096051396456548960235807424574591137899064492469253437014634020540483865739320844889494109394781110772398094821008622048492572157683566757872977228624456846736259354106130201211258511009327315538515216866064453285121788948776103406234207215444605436154181700356276370670917472857294135410338331529454860580972438187298889240292383, 23786164037764255104776575078875800859150492769047667955595841258455291831332681962045535652282332847833575993402949967399671426008433793147340878472289554394554111110627070862215166871538798162208233344397426448234476617800807278005785212750424710467166176988255252161880740439352673774301031931168011764889912831056267200408523089971849395809869409128691718343378986656622929647249316951368459618121098593332453306809261810257330023169162436429525679644131543332375145575590349602393497027119672242408015540358088944515149285253280621794581072020473941130722341368772523146751702345305669351769420395554296149274427, 17848157140791838665961911825128750268043108939621984916050400046053503360692600901270602255353989495908812096478378848413110202750937818974641716601824374585246722904911088793574661342835280517956467023395204638837446074442111460676060322959715615003297731751604876657344563922178026566371316356682896403735341088527333919934393978858658398380551954981937917129057087573833435348097393228370408184304551360217494962140543778315855537866500847631223607121899848928878933690140369110779307529661247898676865531529120898647196818208239095405244429079697036990913206954026597187630338125549544775052524022433530890662787, 15035039019312894402409842314467557138832343903338465631567203017335105855992303084989119416358384510733361676193186600590564247499683117558462505796144535706576044376043555204675103736314469394182563220778922443464771576077602373341769964205342090020802272037729122881955928044886469249454894583004588864697545684247289137893850383540284648881306586175179971868478801134356601955934834619373094323781381509201747059620553038825649754232385125143894973297133423965151474125174071155425510439709419245469344230014851083303152425593712211007876119013994837148368299537544999202089428584569936003140584800017587385395267, 15541793225731870574739431785934032173003939450438556256970240632756600091000042160333171637658817714129618120448340870225445947580014911237102166713078106390876060339486190750998743664808290835267126699021565784201024563729172455249488202533148812125371654198774167532314733661099294651753611453281836029678632308536723727202745975903094214077054804233840837341344708354315592447609861435118245021544479053747917410392502574124970582799837213765904114567665418692185796876058448181135619973097694110727745286504877591137938095621708761680477886908016158609033087238197913462136859857432340786933537403713109994560497, 17918721341674731362752252267166778345925698478727108958243319319943121255548243965703060052117632519855758170129634870789600151385362041113666107758810359677562686664987697767160097273838408630762755829931476250878491119811311817814688331993935902052840000825549521105388469819390174500901221195293905636319150632004425439589616873888894170155101124271256860978902476700229203462459820274118263541395156742290849734533088103428056457211373299643951152889134742714282426314381096212503438334790644747219473926339098876337339540765881544409098989337385146183028584964118773447730509401602477293705923547199987688926339, 13209539111148626119487776850729986828541205143731315393931918903053463480136865651288513015530974691132624386997700802608532194191068932996980809650683387547435832026881706457202878096628430168959509355061376664202655089706436494739588707613017547974805229820586519528181761182962237003574485847743617110830593219470455274020782424124856301280287808545356506324918693478212023846982160880547508564725904631697849152786937420955472556465208060174631080613855254502723460257184246172069166268639332377220189253461566200221994452352231953989065445787117219608690796647696675842329718886426638095098242683554473678181721, 13734341134493557538398397084890302170181226262177489345703964913880125209038303423577315958769539643887200565283230997461622015883448028199849225259306823850727614367106138968360396460707162373204337722642426059431494894641281337702961249131391038972162207012759083518858805633226412912987711787051711744411443641995482442418574913182338639196708630824992672024331174773215194031279195301267403892359400228443662671993917804412036597667554610322886218468573055645597020735034776386034517130785525749424516995061709607604702321543573989466472992251796010547469240463283109698319101282353733428506634576183912724827891, 16436737454526802785135789027333189807877166303913261923968431850613775688409733282029899804469781337529768664555348439173055869832736997725357958860882964449445365274560647200154211459598402038733389627182558553562681098111398179694103176541937195877583677018641893228556431649894739140538653393250905198658734900966767871056056727778583415526142003270541065581241133638163268634580640675512277817223807673850939566776083643793878171930052517720645026911522247991864352650040584944456823879774096723091229541696157755415322809098772518709650904141520589814947985154340534056063842332102043708575808353450050327764167, 18404123323369643600762965721576519074811426080878467798897413842312790986118237173450810456149927139734904634260847862659236763196325362561597871319296908024987697892188375548008270536353067153212887390099898259047413044787519532967208377251125759567919286195478401875862305482098773031552468695032825677653790685910439568128660041619323705747414458104418541717740215667972432591146332066504735367149361856516353727408329156956336876814625252324265824875160253650226517816087503448882846122192869248879125760290285643189122746143832017100414708259748986853640461085329457293431146631548418195989166772296558450523073, 18337766829052845837331669602783216057247058814729480397164793496321598610021065172827339335797586612623724156528246329121163529651093939859348991566036227874855427550141894464471246901563316395391236911370059245439254334970196199146238793649772098033538867269063511574093189420178426616567103011062873054164448802224439890218975825088029311447537062041560277284473905228844035830011420314406193397305490960482540846076615762259657738719209293160927846492838240330278790316471482659243463606720181875534723608785160902570910297084235459071314853567485057861660598535453855155507108934279792610620642990288400230318347, 16243319245891122218594670978889630412868202794054410539686511127050589921547939524013692949546855233439313735890289283965369686121552919669456935935487103977449990222091167560436237218427570183903443244767284488233685780403557745473099784652994279073662057799310527759747801413128873153764977770120271709928451697532471166596375636687794901876951711155445639038185013712601336504971494952441672693753830907552810614152200725155796252881880100765160681980314322322294457197573205309351518593307973761039756993739088930975841383258778148577171654924303446324069738640843268814140980529592088418481316411033275347258959, 19734939349941655428839964575331223817500317825887315180827514084093744517705667141635687796853323502263236346927173270683853320836745928525242095475749921614793650061281041696361002818423460720051832148426592241960683108973204078478472602618456878596107128931041202957699429973906027794744117297316341284659167792272950959651425656007442205536618147877661406783794807467129081296666013243995358641714914130488783374673031208536015906387568969029070330670254874487709626187579010292869972041067739502996487241763605887599140567529908117437267147788522511143563510849217671483937833040242681623966561573103936749004027, 10533813489164957690929934976994806647569531413130206474505522919472783854457527574350069122030327919162218807241132372919036318755493508604974295568964438941063038027090072320251109862373018700809860760699697293402381825858510545734268461142317708168985787041416594465502361412834562926996281831105716411448148405341062577910040015508894661587407128747030287160447161028141460666066063691919964797568756715144381021605259136668108498992906017812641306197210844318957646903752864656816337911844118821650604960544003236118218589344508945500738730122633896731575755167138207098629774819961169270521863611573548360030629, 17809117115655185535035131145051598110670989506851876756715417741792233895570491541474122577903625239143146133845319273032379502433481829386040385875065091456630825494136552843791796682636075997441111265865381885981288502521765957112049155148226214485521790242660331408274121483915140577155425055206428730420416497599466055863168192560246325722676440541947496677575427708326308026955780576203438103134077785011557616213397010914701740346736583851065267406410401457283345178730606945989357861519828439486286085613625017234831937476184453168499614465181921590429346896923110873043633753736625114120944243287964161525159, 14659443783052725371622307518342591437628747308880306425939403273791830331505588117758624421661915613063823487201375699942729051224309126342156548508358054546635605742401146483074301229259782930343124969942084107051022121831984859697793405791931234462028023815074917785534942110026752987021297636159488237489755066585419706884532585916162235277154424455384896603555262095681483670061405842560285530098877249745603826595250577201677257702016760430121708068239251310123736939475835755141548897929450788120284432220388685464548873171056287363746363521811282455821531904777940639720714711525999407687191043305289782989819, 22861882883346221299793892320702887556011173607906298583834373982968942569432178512980838750042344891554850567146418808864650677764649276811506025391827959010728227994292669112343815160050795991064067283230130103862486296983558073017806607393723920517772902060781105099183328019502704656542427486610333148878601552098789025506370366655673141092282000960160760017213072481327301616453129608521676762499847688997454610769443561246448711718775992581054848542343048052995609777941171396083317063386291582205768213422455385271652250527145214626437066160519184770710679504353151223757040673483130288800175327187938145399819, 20432603271791504670103641591495943883342030720883027451137042465848430975239817610296002513103231023136718046769357073850238541752386234262779550781595509796260197451934257285116164273232230442917345977268552821186430634239583081630801831876244586606748588810071318361155821607633490488412049585252535126017994226251855901419989564419519390339871896507508266689447432305514676099508750630002704051789757907278692466165683207470583356186195053913456949964440713272973375647933335255321829267662062989995488541422253487016667189455723201988493088923280725859330676129453133240849899655082701657878442136359597425431361, 27165694191205433163631631386694567462710980772083552879067695355772170020005900772857581838149608599905579142631758216372675809623523899337839362723719950146385243503348604130649830252109410021158807236677879722910805699923314447774368864383936555872747887813778695558808580422200172353852588546710689419958957893130886824256013176152593909031801899217812278148463010801700307779942697255505293705685555885737263889443761655725234221383779827035242913283330805777169410324767798110479767826418813095243185951423291075073253901465239779304393719105326619715207847788498134802136931767504812303602672354503052583857849, 14224395012914122158565611537070994961931807525112860131982488051870241068561811543227389773251110914209000801753190509134588114366503656975342652813137215899066541462180318895027136492378140447871641494309596344872361743836476421651952272866694890338605906672486849936365069045185160926064791461018564839664069829154440191177082428159428724927827480596897894021085748916556111423669127829318644437084872641719356066654750760116406562742229571692388234394819641718505978901671544499200131672960273707938676045458054840643850650675232776882454673191618296152392868591469857181514093078881685120119063977011298589479477, 10078020103521371909276825041988862051239134726920762029953115182367478016654230690937326975227395771783349557533480363020870226581838293570302047261125062495592470637732781229968258499981177771751423046704316328624784533246279548544582242067829360037895597609649454467187384297057992182396468504644068237173029080696251897015916592399782657126102232041098037117235053871151136050998749080444040746998403141208175431885262143751435831206092839769764117824577637184338323895419706786322027803437786877881942038257014810177440590081207114563986944999834165942591756252952467544784845390912448984146016085128271695963229, 21823032289406853868423766709001064532021807711941272140196423268208188591229137718733533826687308672875177573849006150914697546160928095822557751663839658261274174815404175079486081835657497233214402708062984325280398967314853360727702818002222310737142034615807928141402924718536664255020533481423460039629733330163749585594890049940718519984001467258000359129444872049872813946054549484530510276846693363015410859251213787579732874832230779199832874919233738751651441450970930486019658576429290671776064556541375910005356600336799440032032947958363136057585680484611140038205246323927471677811182203405043892192653, 10894760034718720583467577815044370159365572126220897151327929203287954749760914701089503398543571538532798643265043092107432576593151944859996434946157003115185803845335367610968181733350514490529327740010018087647348748881620017155148014389900760147273010017297532724627774695245124032481669579782062745503338855715708133958894252018855019791504435505449673621559255102078979466698771031283141029068637645615384521163884655657427856595551845713993297052858694459300738454829125753951705794759876364147112454073357249300176990513470197281969028008036071643074148162554251122213852030701856323962043684870349211998203, 16826133750782824210441465302551942937492009770238095360453526842192831470368083568161711830096135991538233722613244278073369627961981474572810918605084299373512772761910377274908545468080216502156298358957682637585644161842670250379703193749363898693840298822540115873257058438430449581571845806364521439164590644699913333750839580055388831866583537813441764626337490297700898314971807442881387888253001941175591010080358997530087931447043139965584580815270833495850730588024198079685926878575472244358576507883418730485334129233939731647531414866622483910422672223974950145228069888558582379026765733850268714805497]
for n1 in n:
for n2 in n:
if n1 == n2:
continue
else:
if gcd(n1, n2) != 1:
print("Not all are coprime!")
break
c_prime = crt(c, n)
m = c_prime.nth_root(e)
print(long_to_bytes(int(m)))
## b'grodno{I_s3nd_y0u_gr33t1ngs,_long-no5ed_b4rb@rian!}'Speeding up RSA
## FastRSA.txt
from Crypto.Util.number import getPrime, isPrime, bytes_to_long
from random import shuffle, randint
from secret import flag
flag = bytes_to_long(flag)
def GenerateModulo():
p = getPrime(512)
res = [q for q in range(p, p+100, 2) if isPrime(q)]
shuffle(res)
return (p, res[0])
p, q = GenerateModulo()
n = p * q
e = 65537
ciphertext = pow(flag, e, n)
print(f"n = {n}")
print(f"e = {e}")
print(f"ciphertext = {ciphertext}")
This is a Python code, I don't know why it is saved as a txt file :/
Anyway, FastRSA.txt tells us that $p$ and $q$ are quite close, namely $p < q < p+100$, which we can solve as follows:
So, we can first sample a prime less than $\sqrt{n}$, divide $n$ with it, and test whether the result is also prime, yet the difference is within $100$. Surprisingly, the largest prime less than $\sqrt{n}$ (which can be found as previous_prime(floor(x)) in Python) turns out to be a divisor of $n$, kindly allowing us not to have to go through multiple rounds of trial-and-errors!
from Crypto.Util.number import getPrime, isPrime, bytes_to_long, long_to_bytes
n = 68022741432432659084802752907723896845807597528827093397040482890296955569957917533647208679014132848196640022782537553867867116789555103992690960043358529714577060390999199352850076508734027336995147674705206553971423041116507591767092936323207651404971678259040137037188349250850647087365720392427587716357
e = 65537
ciphertext = 33645617730925667540706843258029945045275653793905004841831372367593972949577825491212282337168392705134683986040003011405449559098226368343868360682321377784836699252707573555021829931008096967637686723813766415931847878736794077491708783671648158579854763189010308346516641122365460325044193705398891622627
n_real = 68022741432432659084802752907723896845807597528827093397040482890296955569957917533647208679014132848196640022782537553867867116789555103992690960043358529714577060390999199352850076508734027336995147674705206553971423041116507591767092936323207651404971678259040137037188349250850647087365720392427587716357.0
x = n_real.nth_root(2)
p_candidate = previous_prime(floor(x))
q_candidate = n // p_candidate
assert q_candidate > p_candidate
assert q_candidate - p_candidate < 100
phi_n = (p_candidate - 1) * (q_candidate - 1)
d = e.inverse_mod(phi_n)
m = pow(ciphertext, d, n)
print(long_to_bytes(int(m)))
## b'grodno{Ofru*YgePg8h}'
Flag: grodno{Ofru*YgePg8h}
RSA. Don’t you see?

This probably was my second least favorite chal.
bad_key_RSA7.txt contains modulus $n$ and ciphertext $c$.
## FastRSA.txt
n = 510455968498862752142013731579474328723310777296251103995720014690922544772970221326609943932666933884583779989279749751965065759326718241861261266118931632314278216558197999744401997064607812611656202982537707422336316278240818112605133350665090469282358420767497684038370214831241610948332950200948893154418227177756661105178181344918831905709071807822815920145833475947583975940930708656865134570100826908846882042480273905993605262506238894653889076488054769060548390264030368213974838640283290652810034721062024772512570469656593296183132887893008387954382307012480402982539766107913546246342536372712823848005080430374027732201643609667812026739871057278001851403896353883323140311508803529006106549270303682588173140904015031303721807528619688027406527232487050011016079831657471193756667793724441364661954794745690554595751283917370080658925469370380727815766735405592012955326943595828938713062234746000895077621037608721684995119817829484718653817230220705751287420365781471942393843166891317525257821901962245090503999770832372884893224189945428758494073216783176892424245758369646363325179308507434383283640229263136296101396815852592981728133820291727435434173738862100819440625756334619060411057040087732583209603106650509993277189670378133215245690678106477277633362769064603979510781409762235829530175058778095982186310999563997968042998587278325447511129924286555795264462773734226498045541962580476621356090136504314596552452013121685061373469857477073805740867028448268443972695736905371988108610381428537873504771426161043127036299220264496866932405323908848839098360231461768903038258186478712005777780041606910730043539001228290271381595228100424427247479313848996067119856933463904530738266923484015939440490383017021789690413905437661284762742673909462218623073915597832399887644502779555022245760357198611534125609390567760580946179110263015926341677522153296600234195258663133107810476321446293325720989139998505352336490794509096366318974917903790909095308400678705082307448439651342933203683211220006159444557921006752617792409868741054755642124403082575553056416560150393879360813285957295794522756798177134654677518050479567582642692122853242389362860671141734035679201354670378865192887096975058036154819057923758044248841912696220411199154448555418294647711081902386844160478032141479071012268929133154462253116123338321383889967758974217473298926308739099841117520373845644945058295972634625329709675667497065410925495130269882523507
c = 146191992513246362469507704007583693878019668405112522434911516253897250863564984597502119212030542733240884634727607094051644988000371061167046076333035170258569378315089526140301960546749921731405886181318781589070874855288644318994081011862448500882176793820654331181792725059180024358540975190199239355030050554843485368434873252779289350203984223248843741661015758452258454711183342915926826470953793097295187270157574352590083347620756837006702652224468440461390408764820318857423862757287894502424794108994242765807437302875671703409225533491419983884889187539685536993337825182665553664889009910421535551727817328796926973615135952284983962338591255274394713205663577280389714423036732807416048296721177841516090446642609898509936030583184449262932434371025684043715748591270141139404342719082255845746904063234079151421242737516426820631107635564101471481703690740771977770299935664223033324972107308225574043263600523027644072208042951082226524195927434141678229967397193267969519691477229896804777542037308265803982451500287490173430299183788034036630885563720426543493038308837226297161620483490688118616912687406119854625466739572707081021141379403692566538617619349196628880991899189160253188197361086687625067108099589867715155511594230501980229866087983639664181917072288745344286526893180632809747290366617411413214567287911361246947758885723761297732171318229199138290975135908385825468275755860842078088991004706664332947073131545716673449119648202529785484100747417496022257588619870489887983811642162265016298539495576653063474402471625911423596708968640071272267843041692972557634311023902678207332392991620539330192731805730024190561956257671227971511704915376259931611983251839476812339073276851362557221748175411112090575001845291274436480893145416887304425699546900018980380483932834041147311814295978324353531302933018286315592594086089933639954151713470691045218438547455727127045177566679338154853805948333367100928698494950018394825821209720037145786375735666562089611447195387615418387417717680311902983589536196637143290373
Running print(len(bin(n))) and sp.isprime(n), we can find out that $n$ is a 8191-bit composite number. Wow! My computer won't stand a chance of factoring it.
So, yes, $n$ is massive, and yes, trying to factor it yourself could melt your RAM (of your computer or your brain), but because $n$ is massive, $c$ seems very small compared to $n$. This means there is a possibility that $m$ is, like, very, very small.
Factordb says $c$ is a power of $43$, in particular:
\[c = (590578 \cdots 663997)^{43}\]and we know that 43 is a prime. So it is likely that, $e = 43$ and $m$ is whatever inside the parentheses? Well, one can only try it out!
print(long_to_bytes(590578037986257002656994110209456873232307663997))
# b'grodno{1rt46te362y4}'
Turns out that indeed was the case. I feel like this chal was kind of too guessy... but whatever.
Flag: grodno{1rt46te362y4}
Like a simple RSA
This was my least favorite chal.
## Asim_en.py
from random import randint
def gen_key():
a, b, c, d = randint(3 * 64), randint(4 * 64), randint(5 * 64), randint(6 * 64)
e = a * b - 1
f = c * e + a + e
g = d * e + b * f
h = c * d * e + a * d + c * b + g * g
public_key = (h, f)
private_key = g
key = (public_key, private_key)
return key
def encrypt(m, public_key):
c = (m * public_key[1]) % public_key[0]
return c
def decrypt(c, public_key, private_key):
m = (c * private_key) % public_key[0]
return m
## Asim_en_data.txt
h = 8470387347298476177456807592234800305223146039241805029722152502623609066137655800632000167660507958129073278126249206662322559690599099900670113252751054479281818630329178438136876189437058031446326100810231155131782952040600724
f = 6416887830534433629567050229667684734973282397714251811755752025377169146409477365161229363756766441347368380751372023179641944107478195964183801916988232697767349642657617
C = 4501577816736015596060497850546201260925821617971707200151522683849342994222685636584343269899367495933875369681542486925080096048706520947165012158736670485935607004216130611982263313862618848808033812929735326651289123228929207
I think C is a typo of c in Asim_en_data.txt.
This problem was a bit tricky in an inefficient sense. After opening the file Asim_en.py, you'd start panicking because $e$, $f$, $g$, and $h$ cannot be written in a simplified form; even worse, you don't even know what $a$, $b$, $c$, and $d$ are equal to!
But the thing is, $c = (m \cdot f) \mod h$ and we are given $f$ and $g$ in the Asim_en_data.txt file. Why is this "the thing"? Well, that's all you need!
g = pow(f, -1, h)
m = (C * g) % h
print(long_to_bytes(m))
# b'}syek_owt_sesu_noitpyrcne_cirtemmysA{ondorg'
At first sight, this looks like gibberish, and you might think that this is not the answer and you did something wrong. But it actually is, you just have to flip it.
m_bytes = long_to_bytes(m)
flipped_m = ['0'] * len(m_bytes)
for i in range(0, len(m_bytes)):
flipped_m[i] = m_bytes[len(m_bytes) - i - 1]
flipped_m_string = b''.join([long_to_bytes(byte) for byte in flipped_m])
print(flipped_m_string)
# b'grodno{Asymmetric_encryption_uses_two_keys}'
Obfuscation is certainly a valid direction of making challenges, but this was neither interesting nor inspirational. I also don't think it is the most efficient way. But I might be misunderstanding the true intention behind it, so let's just leave it at that.
Flag: grodno{Asymmetric_encryption_uses_two_keys}
Tabular integral

This is a continuation of As a programmer... chal. The modulus $n$ is the same as well.
## code-1_RSA.py
from Crypto.Util.number import getPrime , bytes_to_long , GCD
import random
random.seed()
flag = b'grodno{fake_flag}'
KEY_SIZE = 512
RSA_E = 65535
def gen_RSA_params(N, e):
while True:
p, q = getPrime(N), getPrime(N)
if GCD(e, (p - 1) * (q - 1)) == 1: break
n = p * q
check(p, q, n)
return (p, q, n)
def check(p, q, n):
a_ = random.randint(1, 100000)
b_ = random.randint(1, 100000)
c_ = random.randint(1, 100000)
d_ = random.randint(1, 100000)
s = pow_m(p, pow_m(q, a_, c_ * (p - 1) * (q - 1)), n)
t = pow_m(q, pow_m(p, b_, d_ * (p - 1) * (q - 1)), n)
result = s + t
print(f"result = {result}")
def pow_m(base, degree, module):
degree = bin(degree)[2:]
r = 1
for i in range(len(degree) - 1, -1, -1):
r = (r * base ** int(degree[i])) % module
base = (base ** 2) % module
return r
dp, q, n = gen_RSA_params(KEY_SIZE, RSA_E)
m = bytes_to_long(flag)
c = pow(m, RSA_E, n)
print(f"e = {RSA_E}")
print(f"n = {n}")
print(f"c = {c}")
## output-1_RSA.txt
result = 20117592692127098588753437379069003348613839573307328479253068975449684582657055021953308835068569396945974471202929298236980403722500726250752177385185136
e = 65535
n = 100453988882542992490998347280864651674523730326071992099923705624297492995724040273435666400892240650403709184653269170214775367155421267297513519983583974127607248712584793703291706765449984242862266005990641621934762324500510163811305939549791463415426045133627623936872711576456064088395298011550598173543
c = 646098991936071165618855133467386214077692769952480307735059513755382001181137258371601655593121675955747317908533063393507780027839742582377329066259567529884707434560746088580480291482009810109491307087053030796747330057377805082208943141866814111327643950041391371422557114240842804177952921952124237052
Now we are given a new value called result. Based on our analysis from As a programmer..., given that $n$ is the same, we can guess that result now is $p+q$, its multiple, or $(p+q) + nk$, or some sort.
Running print(len(bin(result))) tells us that result is a 513-bit integer, so it is a sum of two 512-bit integers. Given that it is much smaller than $n$ and its GCD with $n$ is $1$, we can guess confidentially (?) that result is actually equal to $p+q$. Let's try it.
from Crypto.Util.number import bytes_to_long, long_to_bytes
result = ...
e = 65535
n = ...
c = ...
result_inv = result.inverse_mod(n)
phi_N = n - result + 1 # phi(pq) = pq - (p+q) + 1
d = e.inverse_mod(phi_N)
m = pow(c, d, n)
print(long_to_bytes(int(m)))
# b'grodno{Rem3mber_Euler"s_the0rem_and_1ts_con5equenc3s}'
At this point, I am not sure if this was the intended solution (also if my solution for As a programmer... was).
Flag: grodno{Rem3mber_Euler"s_the0rem_and_1ts_con5equenc3s}
Highly ambiguous RSA
The Python file Triple_ambiguous_RSA.py has everything, including the content of Triple_ambiguous_RSA.txt.
## Triple_ambiguous_RSA.py
from Crypto.Util.number import bytes_to_long
n1 = 1852892720062887225761965098961519184717028045747184821229381416690649150175077469195015762879827
e1 = 18712
n2 = 1684786560529453911475754845780536300328197792513126663487817526891350560429162837595257498214731
e2 = 17656
n3 = 1476397917727380110001203955119376017350831987887155549202221944834157018381937476166521375696257
e3 = 19407
c = 611696235674033015624831923566847674953519491228623379258607782032635868791588102056975818050929
flag = b'grodno{REDACTED}'
m = bytes_to_long(flag)
c = pow(m, e1, n1)
c = pow(c, e2, n2)
c = pow(c, e3, n3)
print (f"n1 = {n1}")
print (f"e1 = {e1}")
print (f"n2 = {n2}")
print (f"e2 = {e2}")
print (f"n3 = {n3}")
print (f"e3 = {e3}")
print (f"c = {c}")
# Output
n1 = 1852892720062887225761965098961519184717028045747184821229381416690649150175077469195015762879827
e1 = 18712
n2 = 1684786560529453911475754845780536300328197792513126663487817526891350560429162837595257498214731
e2 = 17656
n3 = 1476397917727380110001203955119376017350831987887155549202221944834157018381937476166521375696257
e3 = 19407
c = 611696235674033015624831923566847674953519491228623379258607782032635868791588102056975818050929
Ciphertext $c$ was computed as follows:
\[\begin{align*} c & = (\underbrace{(m^{e_1} \text{ mod } n_1)^{e_2} \text{ mod } n_2}_{=: c_2})^{e_3} \text{ mod } n_3 \\ & = {c_2}^{e_3} \text{ mod } n_3 \end{align*}\]$n_3$ is prime, so $\phi(n_3) = n_3 - 1$ but $\gcd(n_3 - 1, e_3) = 3 \neq 1$. But instead, we can divide both $n_3 - 1$ and $e_3$ with $3$ and compute the multiplicative inverse of $e_3/3$.
\[\begin{align*} d_3' := \left( \frac{e_3}{3} \right)^{-1} \text{ mod } \frac{n_3 - 1}{3} & \implies d_3' \frac{e_3}{3} = \frac{n_3 - 1}{3} k + 1 \\ & \implies e_3 d_3' = 3 \mod \phi(n_3) \end{align*}\]and hence,
\[\begin{align*} c^{d_3'} & = {c_2}^{e_3 d_3'} \mod n_3 \\ & = {c_2}^3 \mod n_3 \end{align*}\]We can then compute $c_2$ using Sagemath using nth_root function.
gcd3 = math.gcd(e3, n3-1) # 3
d3_prime = pow(e3//gcd3, -1, (n3-1)//gcd3)
c2_cube = pow(c, d3_prime, n3)
K = GF(n3)
a = K(c2_cube)
c2_list = c2_cube.nth_root(3, all=True)
BUT, then at that point, you'd realize that all three $n$'s here are small enough for Sagemath to compute the nth_root within a reasonable time. So, instead of going through all these maths with our hands and brain, we can just let Sagemath do all the big brain stuff for us. Like this:
from Crypto.Util.number import long_to_bytes
import sympy as sp
import math
n1 = ...
e1 = 18712
n2 = ...
e2 = 17656
n3 = ...
e3 = 19407
c = ...
# c = ((m^e1 mod n1)^e2 mod n2)^e3 mod n3
"""
Previous direction
"""
# gcd3 = math.gcd(e3, n3-1) # 3
# d3_prime = pow(e3//gcd3, -1, (n3-1)//gcd3)
# c2_cube = pow(c, d3_prime, n3)
# K = GF(n3)
# a = K(c2_cube)
# c2_list = c2_cube.nth_root(3, all=True)
"""
New direction
"""
K = GF(n3)
c = K(c)
c2_list = c.nth_root(e3, all=True)
K = GF(n2)
c1_list = []
for c2 in c2_list:
c2 = K(c2)
c1_list_i = c2.nth_root(e2, all=True)
c1_list += c1_list_i
K = GF(n1)
m_list = []
for c1 in c1_list:
c1 = K(c1)
m_list_i = c1.nth_root(e1, all=True)
m_list += m_list_i
for m in m_list:
print(long_to_bytes(int(m)))
# b"\xde\x12%\xab\x9a\xfa=\xe8vhA\xe1\xcf\xf0tA\x80\xa3{J'
## PeK!\xc6\xd7cWL\x13U62\xf7\xdc\x9f!\xbd\xd6"
# b'grodno{This_1s_n0t_a_f@k3_fl@g}'
I don't know if this was intended, but I like how they anticipated that there could be more than one solution (possible $m$) and marked the real solution as "not a fake flag."
Flag: grodno{This_1s_n0t_a_f@k3_fl@g}
Ambiguous RSA
This was actually very fun.
## ambiguous_RSA.txt
n = 777756371658356441826729228653092499434631035305172509880322655002004039008045720787492699292349816956024214162682281707332483772214797314033060613323980372951195774893061735986175142948571861677456340554882793376078703872291302030430567132018088785535855408409110377327189973952601340410943042788508253813758310797413184518506957817440212935348105193856735320286761202181863843014473637156803666187315158578927428069529022109186345431842082598475904461332010274125796234390386163234411794022829179847776668959528434596799883850787931364114410352436664187913625065855379249496132986517948363694832630053643957898814106766253069509185062057819464868740755645906236165905410302944050073667197489707292827557882235469313758585436824941776058737561207593994338597243557274586583779294003573579715956405551983309527717168010308210474073655763532261396593836782340235001459323323874331108443898602886777412635264588171440447380273250599296164420162936894801775967062285275415331174008098445058416170315779898002726099868162629427919982038415596943715271451944958290466107472382220610122455028556516287294530657864511238573735141255147514127113474557825358554738290595478206958791661391715249798229726238533489373041633676785713548604217861
e = 50000
c = 277359187737258362457534632897090609560275835679907190105508305441781088814950381016117048539810699066668346328707239514247747907024858310042465519804872870468645205535199652666860215144396517509831499728224333577993959380695379150844556883688676144218513768298762581885211876375391342455796156456940548741775950266259611168974452206230570494668698573109274627591842683500384555496015872119947324253901120166868283565117432214783776347994180900043829861747583679841893145482535708198926172748189296275575298131314037764131458195690034230771810286866816955794935414105559326348029049747362599528397557590649155979645823782983966182573456965073532051120287778829594508586835614410719154415803215604015687922794249575275088281033853893589312980289714947975117796646193511911511459440764242386211925662924184898808246988788167092186489240112034940356104882149267058764103175974317576790173813320755017793253366071995395701277842820830242038217541557382036257895686016950644008318986563083604553889153070592017254562516835720872613177777139282977415232050406102429719686895830799282348962471590476649961821249207276558353697914498653389130863975927905580766179709281500497070076138657086424222192427642911863924117001924531455220929197873
Despite the similarity in the titles, this chal actually is not quite similar to the previous one (Highly ambiguous RSA).
Good news is that $n$ is a prime number. This can be confirmed by using Factordb or just running sp.isprime(n). However, very bad news is that $n$ is a 4096-bit prime number. Hence, naively running m = c.nth_root(e) on Sagemath would take forever! (I let it run for two days for giggles and it could not solve it.)
Factordb also says that
\[\begin{align*} n-1 = 2^2 \times 5 \times 47 \times 8274003953\dots 19 \end{align*}\]and hence we know $g := \gcd(e,n-1) = 20$. The good news here is that $\gcd(e, (n-1)/g)) = 1$ so $d' := e^{-1} \text{ mod } (n-1)/g$ exists, i.e. there exists $k \in \mathbb{Z}$ such that:
\[\begin{align*} ed' = \frac{n-1}{g} k + 1 \implies e gd' = (n-1)k + g \end{align*}\]and this implies, by Fermat's little theorem,
\[\begin{align*} & c^{gd'} = m^{e gd'} = m^{(n-1)k + g} = m^{g} \mod n \end{align*}\]which means that $m$ would be a $g$-th root of $c^{gd'}$ in $\mathbb{F}_n$. Let $\rho$ be a nontrivial $g$-th root of unity over $\mathbb{F}_n$ (i.e., $\rho^g = 1 \text{ mod } n$ where $\rho \neq 1 \text{ mod } n$). Then for some integer $k$,
\[\begin{align*} m' := c^{d'} = m \rho^k \mod n \end{align*}\]It is easy to see that $m'$ is a "candidate" $m$:
\[\begin{align*} (m')^e = m^e \rho^{ek} = m^e = c \mod n \end{align*}\]because $\rho^{ek} = 1 \text{ mod } n$ since $g \mid e$.
n = ...
e = 50000
c = ...
g = gcd(e, n-1) # 20
d_prime = (e).inverse_mod((n-1)//g) # e d' = ((n-1)/g) k + 1
m_prime = pow(c, d_prime, n)
assert pow(m_prime, e, n) == c # True
But there is no guarantee that this $m'$ (denoted as m_prime in the code above) is the true $m$ that we are looking for. As $\mathbb{F}_n$ here is a field, there can be (up to) $e$ distinct solutions to the equation $c = m^e \text{ mod } n$. They can be found by multiplying $e$-th roots of unity to a $m$ that satisfies the equation.
Let $\zeta$ be a non-trivial $e$-th root of unity over $\mathbb{F}_n$. Since $\zeta \in \mathbb{F}_n$, its order should be divisible by $n-1$ by Lagrange theorem (because $\left< \zeta \right>$ would be a subgroup of $\mathbb{F}_n^{\times}$). Hence, the order of $\zeta$ should be divisible by both $e$ and $n-1$ and hence should be divisible by $\gcd(e, n-1) = g$. So finding a non-trivial $\zeta$ such that $\zeta^{g} = 1 \text{ mod } n$ is sufficient because we can use that to generate subgroup $E := \left< \zeta \right> \subseteq \mathbb{F}_n^\times$ that consists of all $g$-th root of unity.
And because of this, we actually do not need to introduce and use this new variable $\zeta$, because it is exactly $\rho$ in the end. Also, since $g < n$ yet $n$ is prime, every element of $E$ here should be unique (i.e., they are primitive roots of unity) and it contains all elements whose order is a factor of $g$, not just $g$.
However, now the question is: how do we go about finding $\rho$?
Let $r \in \mathbb{F}_n^\times$ and $r_E := r^{(n-1)/g} \text{ mod } n$. Clearly $r_E^g = r^{n-1} = 1 \text{ mod } n$, and so $r_E$ is a candidate primitive $g$-th root of unity. And to test whether $r_E$ indeed is a primitive $g$-th root of unity, we can calculate the cardinality of $\left< r_E \right> = \{ r_E, r_E^2, \cdots, r_E^g = 1 \}$ and make sure it is $g$ indeed. Oh, and of course, both $r$ and $r_E$ should not be $1$, you know what I meant ![]()
r = 1
r_E = 1
while r_E == 1:
r += 1
r_E = pow(r, (n-1) // g, n)
print("r =", r) # r = 2
# r is x such that x^20 = 1 mod n
gen_by_r_E = []
for i in range(0, 21):
r_E_i = pow(r_E, i, n)
if r_E_i not in gen_by_r_E:
gen_by_r_E.append(r_E_i)
print("abs(<r_E>) =", len(gen_by_r_E)) # abs(<r_E>) = 20
That very well was the case, and now we can set $\rho = r_E$. Now, with one $m$ such that $m^g = c \text{ mod } n$ that we found already, we can multiply it with each element of $\left< \rho \right>$ and it will be another solution to the equation $x^g = c \text{ mod } n$ because
\[(m \rho^i)^g = m^g (\rho^g)^i = m^g 1^i = m^g = c \mod n\]for all $i = 1,2,\dots,g-1$, in other words, for all $\rho^i \in \left<\rho\right>$.
for i in range(0,g):
m = Mod(m_prime * pow(r_E, i, n), n)
assert pow(m, e, n) == c
if b'grodno{' in long_to_bytes(int(m)):
print(i) # When i = 7
print(" ", long_to_bytes(int(m)))
## b"RSA remains a vital tool in safeguarding sensitive data,
## bolstering cybersecurity efforts, and shaping the digital
## landscape of tomorrow. grodno{Und3rstanding_RSA's_pr1nciples
## _@nd_its_practical_@pplic@tions} empowers us to embrace the
## power of encryption and secure our digital future."
Flag, at long last.
Flag: grodno{Und3rstanding_RSA's_pr1nciples_@nd_its_practical_@pplic@tions}
For completeness, the full solution script is provided below:
sol.py (Click to expand)
## sol.py
from Crypto.Util.number import long_to_bytes
n = ...
e = 50000
c = ...
g = gcd(e, n-1) # 20
d_prime = (e).inverse_mod((n-1)//g) # e d' = ((n-1)/g) k + 1
m_prime = pow(c, d_prime, n)
assert pow(m_prime, e, n) == c # True
r = 1
r_E = 1
while r_E == 1:
r += 1
r_E = pow(r, (n-1) // g, n)
print("r =", r) # r = 2
# r is x such that x^20 = 1 mod n
gen_by_r_E = []
for i in range(0, 21):
r_E_i = pow(r_E, i, n)
if r_E_i not in gen_by_r_E:
gen_by_r_E.append(r_E_i)
print("abs(<r_E>) =", len(gen_by_r_E)) # abs(<r_E>)= 20
for i in range(0,g):
m = Mod(m_prime * pow(r_E, i, n), n)
assert pow(m, e, n) == c
if b'grodno{' in long_to_bytes(int(m)):
print("When i =", i) # When i = 7
print(" ", long_to_bytes(int(m)))
## b"RSA remains a vital tool in safeguarding sensitive data,
## bolstering cybersecurity efforts, and shaping the digital
## landscape of tomorrow. grodno{Und3rstanding_RSA's_pr1nciples
## _@nd_its_practical_@pplic@tions} empowers us to embrace the
## power of encryption and secure our digital future."One of my colleagues pointed out that the fact that $c^{d'} = m'$ might not be the same as "true" $m$ could be a bit counter-intuitive to some people, because, as we computed somewhere above
\[(m')^e = c^{ed'} = c = m^e \mod n\]which understandably gives a "vibe" that $m' = m \;\text{ mod } n$ must be the case.
I think this misconception comes from the fact that textbook RSA (more accurately, its encryption function) is bijective, which is attributed to the Chinese Remainder theorem. However, this problem was not quite an instance of (textbook) RSA because $e$ was chosen incorrectly (and $n$ is prime!); instead of taking modulo inverse, we had to compute $e$-th root (more accurately, $g$-th root), which is not unique.
Here is a concrete example, for those who still remain unconvinced.
## example.py
n = 101
e = 36
m = 7
c = pow(m, e, n)
g = gcd(n-1,e) ## 4
d_prime = e.inverse_mod((n-1)//g) ## 16
m_prime = pow(c,d_prime,n)
print(m_prime) ## 31
print(m_prime == m) ## False
However, as we did in the solution, if we compute and multiply roots of unity, we can recover the true $m$.
## example.py continued
r = 1
r_E = 1
while r_E == 1:
r += 1
r_E = pow(r, (n-1) // g, n)
gen_by_r_E = []
for i in range(0, g):
r_E_i = pow(r_E, i, n)
if r_E_i not in gen_by_r_E:
gen_by_r_E.append(r_E_i)
for i in range(0,g):
m = Mod(m_prime * pow(r_E, i, n), n)
print(m)
## 31, 7, 70, 94
Updated: