0xL4ugh CTF 2024 Writeup
Published:
0xL4ugh hosted their CTF twice in 2024: once in February and the other in December. This writeup is for the latter event.
Some challenges were particularly difficult, and I could not solve them on time during the CTF. I only a chance to revisit them in summer, which is why this writeup is late. During the CTF, I worked closely with dm248.
Because the team hosting this CTF is based in Egypt, some of the flags contain statements referencing some ongoing geopolitical events. I should hence make a disclaimer that this post is not intended to be a description or representation of my personal opinions on those matters in any way en messe.
Let's dive in.
MyVault
I love saving my chats with my friends on my laptop but I should protect them, they have info can make you a billionaire 😎, so to protect them well I decided to protect each chat with a different password, so I will protect each one with the year I knew him at and his country (example is 2013brazil) now I’m sure I’m the only one who know these info.
encrypt.py (Click to expand)
## encrypt.py
import base64
import hashlib
from cryptography.fernet import Fernet
# Function to generate a key from the password
def generate_key(password):
# Hash the password to generate a consistent key
password_bytes = password.encode('utf-8')
key = hashlib.sha256(password_bytes).digest() # SHA256 to get a 32-byte key
return base64.urlsafe_b64encode(key) # Fernet requires the key to be in base64 format
# Function to encrypt the file
def encrypt_file(file_name, password):
# Generate a key based on the password
key = generate_key(password)
cipher = Fernet(key)
# Read the original file content
with open(file_name, 'rb') as file:
file_data = file.read()
# Encrypt the data
encrypted_data = cipher.encrypt(file_data)
# Save the encrypted content to a new file
with open(f"encrypted_{file_name}", 'wb') as encrypted_file:
encrypted_file.write(encrypted_data)
print(f"File encrypted successfully! Encrypted file saved as 'encrypted_{file_name}'.")
# Main script
def main():
# Prompt the user for file name and password
file_name = input("Enter the file name to encrypt: ")
password = input("Enter the password to use for encryption: ")
# Encrypt the file
encrypt_file(file_name, password)
if __name__ == "__main__":
main()Files (Click to expand)
## example.txt
hello## encrypted_example.txt
gAAAAABnbrMBJ8nC_S354rhvHP6i-IP1sY78GNB0rekTpa_WJsJrJC5WldeNMHx8S1EXUz5tiRfReMOoC5uBA2BogFmsCt3y3A==## encrypted_friend1.txt
gAAAAABnbM5Bnp9EBbAWzRLlCwaYI0lk4Lrf98EFhH3bLNomZ3BfX_uTDrNnT_QQxRMMPqZQZSMlSp5A037ekQzgSp890sqyYDi3ZWnLqs2MN8jNZ3A_IqQ5Klsx6h54QoygkOXZp69mpz5HI4I3LVCQ7td9b8i9pNgeVMnP_S5kdZa6Y2PqrSr68kKgqf0anLpe7HSgwONZ2-Y18ykj4lo4hdF_2Yv03SSR6J3DhCgdPNaq43x-kS4ejNncl3yGH5p007OvmoQxZJAlZ0B7LBU1_STZ-NNo26EGDYuCm-7kICjqSx_EDhrIO5Kugz_4oMN52uV2U1n9h7bHgsWZRHtUZTV6PjMphvlNRZi-U4TsiVuHjGZvaUebBBicKOh_SQjUOZo9oqOgSjkiOY25DsjsmnebiqXWFix-l_a3u3js_bPcmCGLrGjaFpV-daeRlWyGBbE08sumsTJQTOqYyvs-mziU_3o4F_Or3cTOFlnjO5eiLm4lUXzC_ee061hFMRiyloTzxY4-s9ENTFoH5_PSz_ByQAx4jS58RiIOMUskOA34DtpWRqXsiQLp4eLb2qkOssQI9WX9kn3B-aTPzfousJjGcil4DpMaDPfRqyt76Hy-IQUQVnogiuL9p0N7JK8Xk1MX3G8AoILa6VbhktC7XU0jIpZ1ow==## encrypted_friend2.txt
gAAAAABnbO1sKXf3OsBZ6NSSpYixG15sgWh84orLz_yRRhr-p0sipXYOT2FD5oq_3ZnDg4IS2-ij__CjUrE_Uqpz-ukSsDMoeQXKi65KcUbAlIqDbHoIWnJrdcdVU1qXpOSruFGOZvSRqtbuRCj7mDU2vQmUQLtpOP7j4AlbqZ8gt0PpAFfFsTZzfcPUBNuGhYCZGJRRTZDxyNgF-SPp7eZeRSVms0zjqigicgGT6cyE3cnGhpW3PgvjH_PyedXw1n-QY0cwWcr0E7qbWqUKwIobuR4cMuF04ywI-uMCXH-rSk7tYHqb1h8OC9XDIy5yrXMY8ReI5SOWikL7YkH6eB0w0H12RUAv0OpxJ78nRhNTg_JzTNtaZEjbyl7v6NBEjx-cbVwdMI54jnUbdZjLDknWV_iSWmV40G94rLZy53v3WvdwTbuNoIq6caCXXmehJNPIY7S19x_c3LxsO07msAJQF4x9XLPOnS6j0yEEbVT7Ez55fhbZwGrRXlfPqBBQ_AYH2UgCnZ_708YawCDjqELqqsAse3nfmbn0qWXFd8HQYkepmZvWMG35_h4Trim-fV2_QnIT01TqKRMyOsFTfZybH1Y6EAepzdAJg2oePFCy5StlbhR3vN_1B53rcBZEu0b31Q5iF5qpDaCXx3HI3v8J_VG3aW3WrExxjGQJfrw3XJoMbYLMcWQ=## encrypted_friend3.txt
gAAAAABnbO285CLp59VwjWxb2E0zl3DbvgPG5pbroxMda_OucjsmCDHOPJs8_XZD5C5WfqKvUzE0WkELmDYb6OOOE-uCnKo7iy-XYrZhWXUxQMiui8s7s4qEBfTpOzfzgj3erPD-BSjTwvMH_nZwC3euR9PFTQhoraWUVPfsL61JgFL5uYZMU2lxgxaJHA5Ta_oC19GEhiDJuK9PLjxMWi6_Y1x4OsmGRPu-cfl9PyZYI_XR_-NAU-mMfDe6sKtYHV_YI94Oc-diHBRlXimoHe1J4deJFuS6RKzjq9oS79qF-40C5Hgi2BNAA9DPTqwhYkHrrdty11NzyUAZdn3d1Y9kDVGUgoI48XovDyC4Bz06-grIHbX0qbfTHnhUPwdw7eEvwdS2POrfNqR6B_KBgbcO3Eht5sv8u_-_wfBuiFD0GjShSiDV6pvzIm7MQf4qZtDs-ESnFhDnNlrt8u-vsmpI-t4q3kqKDcYH00TGn2UVrALy0QRGJ5UKpHQeyqICgP07rtHE_9dXszcWWU1INsMQNt3iSY5dw5-ZdcaaUqkqAajEN9xH7HUW3Pqz3SELn_KkZZyujM9OwVKO0rklZqsmfw_CPo9sVg3zH8pGMTXR18e29uOVK9HL5gNUQxtZMiK89obdC0GDR9rkWr6YBJeBDyHnHgBVOw== Brute-forcing all combinations of country and year is certainly feasible. There is also the pycountry package which contains the name of all countries and their associated details. The only thing to be careful is that some countries are named slightly differently in that package: for example, Russia appears as Russian Federation and Turkiye as Turkey (I was told that Turkiye is actually the correct spelling, but apparently the chal authors did not go with that spelling). I realized this only after failing even when trying pycountry.historic_countries which returns the name of countries that no longer exist (e.g., USSR).
## decrypt.py
import base64
import hashlib
from cryptography.fernet import Fernet
import pycountry
# Function to generate a key from the password
def generate_key(password):
# Hash the password to generate a consistent key
password_bytes = password.encode('utf-8')
key = hashlib.sha256(password_bytes).digest() # SHA256 to get a 32-byte key
return base64.urlsafe_b64encode(key) # Fernet requires the key to be in base64 format
# Function to encrypt the file
def decrypt_file(file_name, password):
# Generate a key based on the password
key = generate_key(password)
cipher = Fernet(key)
# Read the original file content
with open(file_name, 'rb') as file:
file_data = file.read()
try:
decrypted_data = cipher.decrypt(file_data)
with open(f"decrypted_{file_name}", 'wb') as decrypted_file:
decrypted_file.write(decrypted_data)
print("success!")
print("key was", password)
except:
# print("unsuccessful")
pass
# Main script
def main():
file_names = ["encrypted_friend"+str(i)+".txt" for i in range(1,4)]
countries = list(pycountry.countries) # + list(pycountry.historic_countries)
years = list(reversed(range(1900, 2025)))
for file_name in file_names:
for year in years:
for country in countries:
password = str(year) + (country.name).lower()
decrypt_file(file_name, password)
try:
password = str(year) + (country.common_name).lower()
decrypt_file(file_name, password)
except:
pass
for country in ["russia", "england", "saudi arabia", "micronesia", "palestine", "turkey"]:
password = str(year) + country
decrypt_file(file_name, password)
if __name__ == "__main__":
main()
# 2005russia
# 2016qatar
# 1980turkey
# 0xL4ugh{sad!__no_easy_challsanymore}
Decrypted files (Click to expand)
## decrypted_encrypted_friend1
Ossama: Are you ready for the next step in the plan?
Mohammed: Yes, everything is set. But we need to make sure no one knows about these details.
Ossama: Of course, we can't afford for anyone to uncover our identities.
Mohammed: We're at a critical stage, but if we succeed, the reward will be massive.
Ossama: That's what we're hoping for. But we must be cautious at every step, and here is your first part of our plan 0xL4ugh{sad!_
## decrypted_encrypted_friend2
Ossama: Do you have any updates on the project?
Khalid: Yes, but I want to remind you to be careful. There are some eyes watching us.
Ossama: Don't worry, the whole team is aware of the situation.
Khalid: But there's something unexpected—there might be leaks from inside the organization.
Ossama: Then we need to change our plans. We can't take any risks, here is the your part _no_easy_challs
Khalid: I'll secure all the channels. Don't worry.
## decrypted_encrypted_friend3
Ossama: Do you remember the secret meeting we had last week?
Ali: Yes, but I need to remind you that any leaks could have severe consequences.
Ossama: We know, that's why I don't allow anyone access to sensitive information, here is your part anymore}
Ali: I hope we have enough time to complete everything before they find out what we're doing.
Ossama: We'll finish everything on time, we just need to work together and stay cautious.Flag: 0xL4ugh{sad!__no_easy_challsanymore}
Capawchino Cafe
challenge.py (Click to expand)
import hashlib
import json
import os
import random
import ecdsa
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
from Crypto.Util.number import bytes_to_long, long_to_bytes
IV = os.urandom(8)
KEY = os.urandom(16)
FLAG = os.environ.get("FLAG", "0xL4ugh{6d656f776d6f65776d6f65776d6f6577}").encode()
class Player:
def __init__(self, credits=0):
self.credits = credits
self.dishes_washed = 0
class CoffeShop:
def __init__(self, available_credits):
self.available = available_credits
self.curve = ecdsa.curves.NIST224p
self.g = self.curve.generator
self.d = random.randint(1, self.curve.order - 1)
self.pubkey = ecdsa.ecdsa.Public_key(self.g, self.g * self.d)
self.privkey = ecdsa.ecdsa.Private_key(self.pubkey, self.d)
self.branch_location = (
int(self.pubkey.point.x()), int(self.pubkey.point.y())
)
self.gen_ks()
def gen_ks(self):
c = [random.randint(1, self.curve.order - 1) for _ in range(6)]
self.ks = [random.randint(1, self.curve.order - 1)]
for i in range(7):
k = int(sum((c[j] * (self.ks[i] ** j)) %
self.curve.order for j in range(6)) % self.curve.order)
self.ks.append(k)
def pay_player(self, player):
credit = "100 EGP"
sha256 = hashlib.sha256()
sha256.update(credit.encode())
hash = bytes_to_long(sha256.digest()) % self.curve.order
player.credits += 100
self.available -= 100
coin = self.privkey.sign(hash, self.ks.pop())
return json.dumps({"s": int(coin.s), "r": int(coin.r)})
def clean(self, data):
plate = data.encode()
cipher = AES.new(KEY, AES.MODE_CTR, nonce=IV)
return cipher.encrypt(plate).hex()
def check_if_clean(self, data, plate):
cipher = AES.new(KEY, AES.MODE_CTR, nonce=IV)
try:
p = json.loads(cipher.decrypt(bytes.fromhex(data)).decode())
m = json.loads(plate)
if p["plate_no"] == m["plate_no"] and p["plate_prop"] == m["plate_prop"]:
return True
except BaseException:
pass
return False
def wash_dishes(self, player):
if shop.available < 100:
return "We're out of money, sorry :c"
plate_no = f"{player.dishes_washed}"
plate_prop = random.randint(1, 9)
plate = json.dumps({"plate_no": plate_no, "plate_prop": plate_prop})
print(f"Please clean the following plate: {plate}")
cleaned = input("(hex) > ")
if self.check_if_clean(cleaned, plate):
player.dishes_washed += 1
print("Here's your cheque: ", end="")
print(self.pay_player(player))
return "Good job! You got 100 EGP."
return "You didn't clean the plate properly! >:c"
def checkout(self, player):
if player.credits >= 800:
print("You have enough money to pay for the meal! c:")
sha256 = hashlib.sha256()
sha256.update(long_to_bytes(self.d))
key = sha256.digest()
iv = os.urandom(16)
cipher = AES.new(key, AES.MODE_CBC, iv)
print(f"Here's your receipt: ")
return iv.hex() + cipher.encrypt(pad(FLAG, 16)).hex()
return "You don't have enough money to pay for the meal! >:c"
print("""Welcome to
____ _ _
/ ___|__ _ _ __ __ ___ _____| |__ (_)_ __ ___
| | / _` | '_ \ / _` \ \ /\ / / __| '_ \| | '_ \ / _ \
| |__| (_| | |_) | (_| |\ V V / (__| | | | | | | | (_) |
\____\__,_| .__/ \__,_| \_/\_/ \___|_| |_|_|_| |_|\___/
____ |_|_
/ ___|__ _ / _| ___
| | / _` | |_ / _ \
| |__| (_| | _| __/
\____\__,_|_| \___|
""")
shop = CoffeShop(800)
you = Player(0)
print(f"Thank you for eating at at our branch in {shop.branch_location}.")
print("Your total is 800 EGP!")
print(f"==== BEEP === YOUR BALANCE IS {you.credits} EGP.")
print("Oh no, you're broke :c, that's okay, you can always wash the dishes for 100 EGP.")
print("Let me show you the ropes!")
print("You will be given a plate, and you're supposed to clean it! Let me do the first one for you.")
plate_no = f"{you.dishes_washed}"
plate_prop = random.randint(1, 9)
plate = json.dumps({"plate_no": plate_no, "plate_prop": plate_prop})
cleaned = shop.clean(plate)
print(f"Dirty plate: {plate}")
print(f"Cleaned plate: {cleaned}")
choices = {1: "Check Balance", 2: "Pay", 3: "Wash Dishes", 4: "Exit"}
while True:
print()
print("Now, what would you like to do?")
for k, v in choices.items():
print(f"{k}. {v}")
try:
choice = int(input("> "))
if choice == 1:
print(f"Your balance is {you.credits} EGP.")
elif choice == 2:
print(shop.checkout(you))
elif choice == 3:
print(shop.wash_dishes(you))
elif choice == 4:
break
else:
print("Invalid choice!")
except:
print("Something went wrong, please try again.")The code is very long, but we just need to pay attention to a few parts. First of all, a dirty plate represents a plaintext, and a cleaned plate represents an AES-CTR encrypted dirty plate.
## From Challenge.py
def clean(self, data):
plate = data.encode()
cipher = AES.new(KEY, AES.MODE_CTR, nonce=IV)
return cipher.encrypt(plate).hex()
...
plate = json.dumps({"plate_no": plate_no, "plate_prop": plate_prop})
cleaned = shop.clean(plate)
Upon inspecting the starter code, it appears that both secret key (KEY) and nonce (IV) are fixed throughout the whole process. This is a huge red flag: it opens a door to AES-CTR nonce reuse attack.
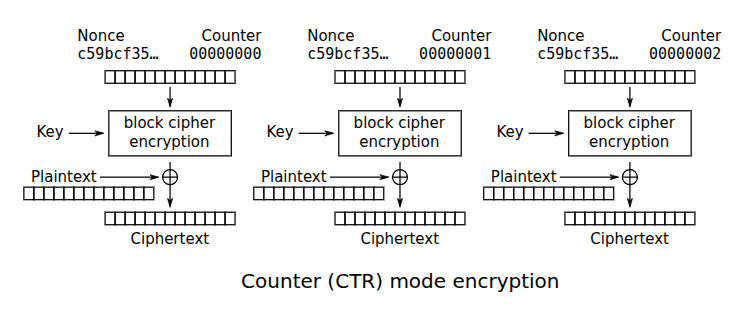
Basically, AES-CTR encrypts the key with nonce, then XORs the encrypted key with the plaintext. \[ \begin{align*} & \texttt{ctxt}_1 = \texttt{ptxt}_1 \oplus \mathsf{AES}(\texttt{KEY}, \texttt{IV}) \\ & \texttt{ctxt}_2 = \texttt{ptxt}_2 \oplus \mathsf{AES}(\texttt{KEY}, \texttt{IV}) \end{align*} \] So, if the same key and nonce are reused, we can cancel the two by XORing them: \[ \begin{align*} \texttt{ctxt}_1 \oplus \texttt{ctxt}_2 & = \texttt{ptxt}_1 \oplus \mathsf{AES}(\texttt{KEY}, \texttt{IV}) \oplus \texttt{ptxt}_2 \oplus \mathsf{AES}(\texttt{KEY}, \texttt{IV}) \\ & = \texttt{ptxt}_1 \oplus \texttt{ptxt}_2 \oplus \mathsf{AES}(\texttt{KEY}, \texttt{IV}) \oplus \mathsf{AES}(\texttt{KEY}, \texttt{IV}) \\ & = \texttt{ptxt}_1 \oplus \texttt{ptxt}_2 \end{align*} \] In our case, we want to 'forge' the ciphertext without knowing the key. But we know the two plaintexts $\texttt{ptxt}_1$ and $\texttt{ptxt}_2$ already, and we also know $\texttt{ctxt}_1$:
## From Challenge.py
print("You will be given a plate, and you're supposed to clean it! Let me do the first one for you.")
plate_no = f"{you.dishes_washed}"
plate_prop = random.randint(1, 9)
plate = json.dumps({"plate_no": plate_no, "plate_prop": plate_prop})
cleaned = shop.clean(plate)
print(f"Dirty plate: {plate}")
print(f"Cleaned plate: {cleaned}")
Hence, by XORing $\texttt{ctxt}_1$ on both sides, \[ \begin{align*} \texttt{ptxt}_1 \oplus \texttt{ptxt}_2 \oplus \texttt{ctxt}_1 & = \texttt{ctxt}_1 \oplus \texttt{ctxt}_2 \oplus \texttt{ctxt}_1 \\ & = \texttt{ctxt}_1 \oplus \texttt{ctxt}_1 \oplus \texttt{ctxt}_2 \\ & = \texttt{ctxt}_2 \end{align*} \] we can retreive the second ciphertext $\texttt{ctxt}_2$ without knowing the key.
## sol_part1.py
def enc_iv_and_ctr(init_plate_no, init_plate_prop, init_cipher):
plate = json.dumps({"plate_no": init_plate_no, "plate_prop": init_plate_prop})
plate = plate.encode()
return bytes_to_long(plate) ^ init_cipher
def enc_plate(plate_no, plate_prop, init_plate_no, init_plate_prop, init_cipher):
plate = json.dumps({"plate_no": plate_no, "plate_prop": plate_prop})
plate = plate.encode()
return hex(bytes_to_long(plate)
^ enc_iv_and_ctr(init_plate_no, init_plate_prop, init_cipher))
## Initial plate
init_plate_no = "0"
init_plate_prop = 7
init_cipher = 0x557d3c1e00d3486d94bcf5af0dc99f0635d4896853bd45b48b314ce4106ce1cd1e89
## Zeroth plate
plate_no = "0"
plate_prop = 8
enc_plate(plate_no, plate_prop, init_plate_no, init_plate_prop, init_cipher)
# Here's your cheque:
# {"s": 6942379853477073704774142087576474862382708715528191074038523108381,
# "r": 7437506340832881608780633632511042990820829922328485508084330047726}
The cheque it returns upon 'washing the dirty dish' successfully gives an elliptic curve vibe. But for now, let us keep going:
## sol_part1.py
plate_no = "1"
plate_prop = 4
enc_plate(plate_no, plate_prop, init_plate_no, init_plate_prop, init_cipher)
# Here's your cheque:
# {"s": 4273344998781938246092013123671497996530221126803228398425552780018,
# "r": 18480087017986508131327551154692592529571481811714520395856162588185}
plate_no = "2"
plate_prop = 1
enc_plate(plate_no, plate_prop, init_plate_no, init_plate_prop, init_cipher)
# Here's your cheque:
# {"s": 17664531396818707679825828857184650749733082825097226486672780956573,
# "r": 25930373620315040638893683699910736647930060592621715795651662184912}
plate_no = "3"
plate_prop = 7
enc_plate(plate_no, plate_prop, init_plate_no, init_plate_prop, init_cipher)
# Here's your cheque:
# {"s": 14553926144082542251660669119115539379382743280705156407201491517976,
# "r": 11808598157407630208563628253083239187111498250294969852498985343940}
plate_no = "4"
plate_prop = 6
enc_plate(plate_no, plate_prop, init_plate_no, init_plate_prop, init_cipher)
# Here's your cheque:
# {"s": 4282031528978091009234105829186697043601006126111435122656658581169,
# "r": 15885368194089812087966828468941654550060309763425566038990965623915}
plate_no = "5"
plate_prop = 8
enc_plate(plate_no, plate_prop, init_plate_no, init_plate_prop, init_cipher)
# Here's your cheque:
# {"s": 19003282835547571157821193766195277694646425172237624858672146272263,
# "r": 4265541798293693156429137547961570160813919569636938858927299270401}
plate_no = "6"
plate_prop = 9
enc_plate(plate_no, plate_prop, init_plate_no, init_plate_prop, init_cipher)
# Here's your cheque:
# {"s": 4407838758925399420725799232512462778052845663731564982901633805173,
# "r": 9064342282622556858810609762808031353573832340320016292916504039585}
plate_no = "7"
plate_prop = 4
enc_plate(plate_no, plate_prop, init_plate_no, init_plate_prop, init_cipher)
# Here's your cheque:
# {"s": 17592559728106193799657828359796543360099563601104283253017253980824,
# "r": 20293260808792473676561419158098386171650673763544147668283834153742}
# Here's your receipt:
#5729075718eb8e7638b0ba4b7b14942deb9f9550f6e59f4db6b83de599f7666b0f3a7e80177cde6aabf04f51ebfb4e3e746916ad755684ce114543835b42e56d
The receipt above actually is the encrypted flag. Its secret key is a SHA256 hash of a number randomly chosen between 1 and the order of the generator of NIST224p elliptic curve.
## From challenge.py
class CoffeShop:
def __init__(self, available_credits):
self.available = available_credits
self.curve = ecdsa.curves.NIST224p
self.g = self.curve.generator
self.d = random.randint(1, self.curve.order - 1)
self.pubkey = ecdsa.ecdsa.Public_key(self.g, self.g * self.d)
self.privkey = ecdsa.ecdsa.Private_key(self.pubkey, self.d)
self.branch_location = (
int(self.pubkey.point.x()), int(self.pubkey.point.y())
)
self.gen_ks()
def gen_ks(self):
c = [random.randint(1, self.curve.order - 1) for _ in range(6)]
self.ks = [random.randint(1, self.curve.order - 1)]
for i in range(7):
k = int(sum((c[j] * (self.ks[i] ** j)) %
self.curve.order for j in range(6)) % self.curve.order)
self.ks.append(k)
...
def checkout(self, player):
if player.credits >= 800:
print("You have enough money to pay for the meal! c:")
sha256 = hashlib.sha256()
sha256.update(long_to_bytes(self.d))
key = sha256.digest()
iv = os.urandom(16)
cipher = AES.new(key, AES.MODE_CBC, iv)
print(f"Here's your receipt: ")
return iv.hex() + cipher.encrypt(pad(FLAG, 16)).hex()
The cheques we have been getting after washing each dishes was an ECDSA signature:
## From challenge.py
def pay_player(self, player):
credit = "100 EGP"
sha256 = hashlib.sha256()
sha256.update(credit.encode())
hash = bytes_to_long(sha256.digest()) % self.curve.order
player.credits += 100
self.available -= 100
coin = self.privkey.sign(hash, self.ks.pop())
return json.dumps({"s": int(coin.s), "r": int(coin.r)})
Let us first save all eight cheques as signatures $\texttt{sig}_0, \texttt{sig}_1, \dots, \texttt{sig}_7$.
## sol_part2.sage
curve = ecdsa.curves.NIST224p
g = curve.generator
d = random.randint(1, curve.order - 1)
credit = "100 EGP"
sha256 = hashlib.sha256()
sha256.update(credit.encode())
hash = bytes_to_long(sha256.digest()) % curve.order
n = curve.order
branch_location = ecdsa.ellipticcurve.PointJacobi(
x=6503732382296231543532569970033457884342589011526661573418463834176,
y = 2809928394869489076680797710871619691274347878793277636524467319552,
z=1,
curve=curve
)
pubkey = ecdsa.ecdsa.Public_key(generator = g, point = branch_location)
sig0 = ecdsa.ecdsa.Signature(
r = 7437506340832881608780633632511042990820829922328485508084330047726,
s = 6942379853477073704774142087576474862382708715528191074038523108381)
sig1 = ecdsa.ecdsa.Signature(
r = 18480087017986508131327551154692592529571481811714520395856162588185,
s = 4273344998781938246092013123671497996530221126803228398425552780018)
sig2 = ecdsa.ecdsa.Signature(
r = 25930373620315040638893683699910736647930060592621715795651662184912,
s = 17664531396818707679825828857184650749733082825097226486672780956573)
sig3 = ecdsa.ecdsa.Signature(
r = 11808598157407630208563628253083239187111498250294969852498985343940,
s = 14553926144082542251660669119115539379382743280705156407201491517976)
sig4 = ecdsa.ecdsa.Signature(
r = 15885368194089812087966828468941654550060309763425566038990965623915,
s = 4282031528978091009234105829186697043601006126111435122656658581169)
sig5 = ecdsa.ecdsa.Signature(
r = 4265541798293693156429137547961570160813919569636938858927299270401,
s = 19003282835547571157821193766195277694646425172237624858672146272263)
sig6 = ecdsa.ecdsa.Signature(
r = 9064342282622556858810609762808031353573832340320016292916504039585,
s = 4407838758925399420725799232512462778052845663731564982901633805173)
sig7 = ecdsa.ecdsa.Signature(
r = 20293260808792473676561419158098386171650673763544147668283834153742,
s = 17592559728106193799657828359796543360099563601104283253017253980824)
# Sanity check
print(pubkey.verifies(hash, sig7)) # True
Reading the code for functions gen_ks and pay_player again, we know that: Each signature was signed using a different key, generated by evaluating a fixed random polynomial of degree 5 at the previous key value. The initial key was chosen uniformly at random, but the polynomial (i.e. coefficients) remains the same for all keys.
## From challenge.py
def gen_ks(self):
c = [random.randint(1, self.curve.order - 1) for _ in range(6)]
self.ks = [random.randint(1, self.curve.order - 1)]
for i in range(7):
k = int(sum((c[j] * (self.ks[i] ** j)) %
self.curve.order for j in range(6)) % self.curve.order)
self.ks.append(k)
...
def pay_player(self, player):
...
coin = self.privkey.sign(hash, self.ks.pop())
return json.dumps({"s": int(coin.s), "r": int(coin.r)})
So we can write each signing keys (elements of the array ks) recursively as follows: \[ \begin{align*} \texttt{ks}_0 & = (\textsf{some random value}) \\ \texttt{ks}_1 & = c_0 \cdot \texttt{ks}_0^0 + c_1 \cdot \texttt{ks}_0^1 + ... + c_5 \cdot \texttt{ks}_0^5 = p(\texttt{ks}_0) \\ \texttt{ks}_2 & = c_0 \cdot \texttt{ks}_1^0 + c_1 \cdot \texttt{ks}_1^1 + ... + c_5 \cdot \texttt{ks}_1^5 = p(\texttt{ks}_1) \\ & \cdots \\ \texttt{ks}_7 & = c_0 \cdot \texttt{ks}_6^0 + c_1 \cdot \texttt{ks}_6^1 + ... + c_5 \cdot \texttt{ks}_6^5 = p(\texttt{ks}_6) \\ \end{align*} \] where $p(x) = c_0 + c_1 x + \cdots + c_5 x^5$ for some fixed constants $c_0, \dots, c_5$.
Note that the keys are 'popped' as they are used, so $\texttt{Sig}_0$ was signed with $\texttt{ks}_7$, $\texttt{Sig}_1$ was signed with $\texttt{ks}_6$, and so on. Recall that our signatures were pairs $(r,s)$; this is actually a standard ECDSA notation. ECDSA works in the following way:
- $r = x \;\text{ mod } n$ where $(x, y) = kg$ where $k$ is random.
- $s = k^{-1} (z+rd) \;\text{ mod } n$ where $z$ is the hash value.
- Return $(r,s)$ as the signature.
We can solve $s$ for $k$, which gives us $k = s^{-1} z + s^{-1} r d \;\text{ mod } n$, and hence we have \[ \begin{align*} \texttt{ks}_7 & = s_0^{-1} z + s_0^{-1} r_0 d \;\text{ mod } n \\ \texttt{ks}_6 & = s_1^{-1} z + s_1^{-1} r_1 d \;\text{ mod } n \\ & \vdots \\ \texttt{ks}_0 & = s_7^{-1} z + s_7^{-1} r_7 d \;\text{ mod } n \\ \end{align*} \] So we can actually compute all keys $\texttt{ks}_i$'s (values in ks, which I will call k_array in my solve script).
## sol_part2.sage
sigs = [sig0, sig1, sig2, sig3, sig4, sig5, sig6, sig7]
a_array = [(pow(sigs[i].s, -1, n) * hash) % n for i in range(0, 8)]
b_array = [(pow(sigs[i].s, -1, n) * sigs[i].r) % n for i in range(0, 8)]
k_array = [a_array[7-i] + b_array[7-i] * x for i in range(0, 8)]
Now that we have all $\texttt{ks}_i$'s, we can plug them into the system of equations $\texttt{ks}_i = p(\texttt{ks}_{i-1})$ and solve for the coefficients $c_j$'s of $p(x)$.
Degree 5 equation requires 6 equations to guarantee the unique solution. The first goal should be to find unique coefficients $c_0, ..., c_5$, then later we solve $\texttt{ks}_7 = p(\texttt{ks}_6)$, i.e. $p(\texttt{ks}_6) - \texttt{ks}_7 = 0$.
## sol_part2.sage
# Pick ks_1 = p(ks_0), ..., ks_6 = p(ks_5)
# => ks = c Ks
R.<x> = PolynomialRing(Zmod(n))
K_matrix = [[k_array[i]**j for j in range(0, 6)] for i in range(0, 6)]
M = MatrixSpace(R, 6, 6)
M_vec = MatrixSpace(R, 6, 1)
K_matrix = M(K_matrix)
k_array_proj = M_vec(k_array[1:7])
c_array = K_matrix.inverse() * k_array_proj
# Now solve ks_7 = p(ks_6) <=> p(ks_6) - ks_7 = 0
pks6_ks7 = a_array[0] + b_array[0] * x # note that ks7 = a0 + b0 * d
for j in range(0, 6):
pks6_ks7 -= c_array[j][0] * (a_array[1] + b_array[1] * x)**j
# c_array[j][0] because c_array is technically a matrix
Then I tried calling d = pks6_ks7.roots(), but it was throwing an error. It turns out this was because pks6_ks7 is a rational function, where roots() is not defined over.
print(type(pks6_ks7))
# <class 'sage.rings.fraction_field_element.FractionFieldElement_1poly_field'>
But there is still some hope left. We can find the roots of the numerator instead!
## sol_part2.sage
d = pks6_ks7.numerator().roots()
ctxt = '5729075718eb8e7638b0ba4b7b14942deb9f9550f6e59f4db6b83de599f7666b0f3a7e80177cde6aabf04f51ebfb4e3e746916ad755684ce114543835b42e56d'
ctxt = binascii.unhexlify(ctxt)
for KEY,_ in d:
sha256 = hashlib.sha256()
sha256.update(long_to_bytes(int(KEY)))
key = sha256.digest()
iv = ctxt[:16]
cipher = AES.new(key, AES.MODE_CBC, iv)
# if b'flag{' in cipher.decrypt(ctxt[16:]):
print(cipher.decrypt(ctxt[16:]))
# b'\xac\x96\x87\xb0t\xf2\t\x97\x18-\xe4 1^\xf9e\xc4\xda\x98\x8e\xdf\xb6\xa7\x97\xc2JoE\x10\xf6\xe7\xd3\xb4\x8c#8d\xf3\xdci\xef\xef\x82<\xb4\x01"\x89'
# b'flag{efz6vLXjr49NnV7OVBpQSI6opucVMqWs}\n\n\n\n\n\n\n\n\n\n'
Flag: flag{efz6vLXjr49NnV7OVBpQSI6opucVMqWs}
I somehow could not get my solve script working during the CTF. Fortunately, dm248 solved it before I did. Later (about a month after the competition), I gave up and asked dm248 for help. He shared his solve script with me. After comparing my code and his, I realized that I forgot to unhexlify the ciphertext. Tough luck.
Anyways, the full solve scripts are provided below, for your viewing pleasure ;)
sol_part1.py (Click to expand)
import json
from Crypto.Cipher import AES
from Crypto.Util.number import bytes_to_long, long_to_bytes
import ecdsa
import hashlib
import random
import json
from Crypto.Cipher import AES
from Crypto.Util.number import bytes_to_long, long_to_bytes
import binascii
def enc_iv_and_ctr(init_plate_no, init_plate_prop, init_cipher):
plate = json.dumps({"plate_no": init_plate_no, "plate_prop": init_plate_prop})
plate = plate.encode()
return bytes_to_long(plate) ^ init_cipher
def enc_plate(plate_no, plate_prop, init_plate_no, init_plate_prop, init_cipher):
plate = json.dumps({"plate_no": plate_no, "plate_prop": plate_prop})
plate = plate.encode()
return hex(bytes_to_long(plate) ^ enc_iv_and_ctr(init_plate_no, init_plate_prop, init_cipher))
init_plate_no = "0"
init_plate_prop = 7
init_cipher = 0x557d3c1e00d3486d94bcf5af0dc99f0635d4896853bd45b48b314ce4106ce1cd1e89
plate_no = "0"
plate_prop = 8
print(enc_plate(plate_no, plate_prop, init_plate_no, init_plate_prop, init_cipher))
# '0x557d3c1e00d3486d94bcf5af0dc99f0635d4896853bd45b48b314ce4106ce1cd1189'
# Here's your cheque: {"s": 6942379853477073704774142087576474862382708715528191074038523108381, "r": 7437506340832881608780633632511042990820829922328485508084330047726}
plate_no = "1"
plate_prop = 4
print(enc_plate(plate_no, plate_prop, init_plate_no, init_plate_prop, init_cipher))
# '0x557d3c1e00d3486d94bcf5af0dc99e0635d4896853bd45b48b314ce4106ce1cd1d89'
# Here's your cheque: {"s": 4273344998781938246092013123671497996530221126803228398425552780018, "r": 18480087017986508131327551154692592529571481811714520395856162588185}
plate_no = "2"
plate_prop = 1
print(enc_plate(plate_no, plate_prop, init_plate_no, init_plate_prop, init_cipher))
# '0x557d3c1e00d3486d94bcf5af0dc99d0635d4896853bd45b48b314ce4106ce1cd1889'
# Here's your cheque: {"s": 17664531396818707679825828857184650749733082825097226486672780956573, "r": 25930373620315040638893683699910736647930060592621715795651662184912}
plate_no = "3"
plate_prop = 7
print(enc_plate(plate_no, plate_prop, init_plate_no, init_plate_prop, init_cipher))
# '0x557d3c1e00d3486d94bcf5af0dc99c0635d4896853bd45b48b314ce4106ce1cd1e89'
# Here's your cheque: {"s": 14553926144082542251660669119115539379382743280705156407201491517976, "r": 11808598157407630208563628253083239187111498250294969852498985343940}
plate_no = "4"
plate_prop = 6
print(enc_plate(plate_no, plate_prop, init_plate_no, init_plate_prop, init_cipher))
# '0x557d3c1e00d3486d94bcf5af0dc99b0635d4896853bd45b48b314ce4106ce1cd1f89'
# Here's your cheque: {"s": 4282031528978091009234105829186697043601006126111435122656658581169, "r": 15885368194089812087966828468941654550060309763425566038990965623915}
plate_no = "5"
plate_prop = 8
print(enc_plate(plate_no, plate_prop, init_plate_no, init_plate_prop, init_cipher))
# '0x557d3c1e00d3486d94bcf5af0dc99a0635d4896853bd45b48b314ce4106ce1cd1189'
# Here's your cheque: {"s": 19003282835547571157821193766195277694646425172237624858672146272263, "r": 4265541798293693156429137547961570160813919569636938858927299270401}
plate_no = "6"
plate_prop = 9
print(enc_plate(plate_no, plate_prop, init_plate_no, init_plate_prop, init_cipher))
# '0x557d3c1e00d3486d94bcf5af0dc9990635d4896853bd45b48b314ce4106ce1cd1089'
# Here's your cheque: {"s": 4407838758925399420725799232512462778052845663731564982901633805173, "r": 9064342282622556858810609762808031353573832340320016292916504039585}
plate_no = "7"
plate_prop = 4
print(enc_plate(plate_no, plate_prop, init_plate_no, init_plate_prop, init_cipher))
# '0x557d3c1e00d3486d94bcf5af0dc9980635d4896853bd45b48b314ce4106ce1cd1d89'
# Here's your cheque: {"s": 17592559728106193799657828359796543360099563601104283253017253980824, "r": 20293260808792473676561419158098386171650673763544147668283834153742}
# Here's your receipt:
#5729075718eb8e7638b0ba4b7b14942deb9f9550f6e59f4db6b83de599f7666b0f3a7e80177cde6aabf04f51ebfb4e3e746916ad755684ce114543835b42e56d
ctxt = b'5729075718eb8e7638b0ba4b7b14942deb9f9550f6e59f4db6b83de599f7666b0f3a7e80177cde6aabf04f51ebfb4e3e746916ad755684ce114543835b42e56d'sol_part2.sage (Click to expand)
import json
from Crypto.Cipher import AES
from Crypto.Util.number import bytes_to_long, long_to_bytes
import ecdsa
import hashlib
import random
import json
from Crypto.Cipher import AES
from Crypto.Util.number import bytes_to_long, long_to_bytes
import binascii
curve = ecdsa.curves.NIST224p
g = curve.generator
d = random.randint(1, curve.order - 1)
print(g.x(), g.y())
# (mpz(19277929113566293071110308034699488026831934219452440156649784352033),
# mpz(19926808758034470970197974370888749184205991990603949537637343198772))
credit = "100 EGP"
sha256 = hashlib.sha256()
sha256.update(credit.encode())
hash = bytes_to_long(sha256.digest()) % curve.order
print(hash) # mpz(17652096005390789500184919532088101572530464893898551787768088100952)
n = curve.order
branch_location = ecdsa.ellipticcurve.PointJacobi(x=6503732382296231543532569970033457884342589011526661573418463834176, y = 2809928394869489076680797710871619691274347878793277636524467319552, z=1, curve=curve)
pubkey = ecdsa.ecdsa.Public_key(generator = g, point = branch_location)
sig0 = ecdsa.ecdsa.Signature(
r = 7437506340832881608780633632511042990820829922328485508084330047726,
s = 6942379853477073704774142087576474862382708715528191074038523108381)
sig1 = ecdsa.ecdsa.Signature(
r = 18480087017986508131327551154692592529571481811714520395856162588185,
s = 4273344998781938246092013123671497996530221126803228398425552780018)
sig2 = ecdsa.ecdsa.Signature(
r = 25930373620315040638893683699910736647930060592621715795651662184912,
s = 17664531396818707679825828857184650749733082825097226486672780956573)
sig3 = ecdsa.ecdsa.Signature(
r = 11808598157407630208563628253083239187111498250294969852498985343940,
s = 14553926144082542251660669119115539379382743280705156407201491517976)
sig4 = ecdsa.ecdsa.Signature(
r = 15885368194089812087966828468941654550060309763425566038990965623915,
s = 4282031528978091009234105829186697043601006126111435122656658581169)
sig5 = ecdsa.ecdsa.Signature(
r = 4265541798293693156429137547961570160813919569636938858927299270401,
s = 19003282835547571157821193766195277694646425172237624858672146272263)
sig6 = ecdsa.ecdsa.Signature(
r = 9064342282622556858810609762808031353573832340320016292916504039585,
s = 4407838758925399420725799232512462778052845663731564982901633805173)
sig7 = ecdsa.ecdsa.Signature(
r = 20293260808792473676561419158098386171650673763544147668283834153742,
s = 17592559728106193799657828359796543360099563601104283253017253980824)
# Sanity check
print(pubkey.verifies(hash, sig7)) # True
sigs = [sig0, sig1, sig2, sig3, sig4, sig5, sig6, sig7]
a_array = [(pow(sigs[i].s, -1, n) * hash) % n for i in range(0, 8)]
b_array = [(pow(sigs[i].s, -1, n) * sigs[i].r) % n for i in range(0, 8)]
k_array = [a_array[7-i] + b_array[7-i] * x for i in range(0, 8)]
# Pick ks_1 = p(ks_0), ..., ks_6 = p(ks_5)
# => ks = c Ks
R.<x> = PolynomialRing(Zmod(n))
K_matrix = [[k_array[i]**j for j in range(0, 6)] for i in range(0, 6)]
M = MatrixSpace(R, 6, 6)
M_vec = MatrixSpace(R, 6, 1)
K_matrix = M(K_matrix)
k_array_proj = M_vec(k_array[1:7])
c_array = K_matrix.inverse() * k_array_proj
# Now solve ks_7 = p(ks_6) <=> p(ks_6) - ks_7 = 0
pks6_ks7 = a_array[0] + b_array[0] * x # note that ks7 = a0 + b0 * d
for j in range(0, 6):
pks6_ks7 -= c_array[j][0] * (a_array[1] + b_array[1] * x)**j
d = pks6_ks7.numerator().roots()
# print(d) # two roots!
ctxt = '5729075718eb8e7638b0ba4b7b14942deb9f9550f6e59f4db6b83de599f7666b0f3a7e80177cde6aabf04f51ebfb4e3e746916ad755684ce114543835b42e56d'
ctxt = binascii.unhexlify(ctxt)
# print(ctxt)
for KEY,_ in d:
sha256 = hashlib.sha256()
sha256.update(long_to_bytes(int(KEY)))
key = sha256.digest()
iv = ctxt[:16]
cipher = AES.new(key, AES.MODE_CBC, iv)
# if b'flag{' in cipher.decrypt(ctxt[16:]):
print(cipher.decrypt(ctxt[16:]))
# b'\xac\x96\x87\xb0t\xf2\t\x97\x18-\xe4 1^\xf9e\xc4\xda\x98\x8e\xdf\xb6\xa7\x97\xc2JoE\x10\xf6\xe7\xd3\xb4\x8c#8d\xf3\xdci\xef\xef\x82<\xb4\x01"\x89'
# b'flag{efz6vLXjr49NnV7OVBpQSI6opucVMqWs}\n\n\n\n\n\n\n\n\n\n'prime_suspects
## challenge.py
from Crypto.Util.number import bytes_to_long
from Crypto.Util.number import getPrime
from SECRET import flag
p = getPrime(1024)
q = getPrime(1024)
n = p * q
e = 0x10001
suspect1 = pow(1234*p + q, 4321, n)
suspect2 = pow(p**2 + 1234, q, n)
suspect3 = pow(bytes_to_long(flag), e, n)
print(f"{n = }")
print(f"{suspect1 = }")
print(f"{suspect2 = }")
print(f"{suspect3 = }")
"""
n = 19839772406592038190388369555693240762538001200560061266337400393390156583067094925964221108025393509323129492181808800544023673275469504815756943291095595848265120220669476825666894482813540241527304775449458006280511430395083776478716286901666159754102681493836770408600291259628536040434644542060008861460420239246675790014643348741981881010487160862738716411889615506716421080697468265585927037843912107880024620419353850828958766380546515595072180248367832537298679740790910760381847091223213725252496813564585753065499199756614019421519942263274322634395687433695110598812240962419691874373000201021934599758797
suspect1 = 5481486211302967857769378509759769524898893113769798571566110518298239375346559533567130904334120310259073521689660742329402669803133955525980601074061060366523204309605656941088516563019896350744848647220202699971933873327122537767517470710991239051145546233486350769062812973389594972516798683040238948422580474396838973908938438667987996165190322222109916886919741191377317838047550364750510197486200306552822564654524636230517193400552655480382550090475112152259065912376331879070271050217631265029575688136893103014397737263756000822849774077743242156386781732974791603691819070298846187429459320822647710620293
suspect2 = 15471195868740783618434039853444325091271961027566455380499276767098755025135594696728733163606916023568535782480341237444034508459734566848020061886214821897207138082654569949589331097642340763425757407284917986100913980642765560090771257023522726807588417681283124019065392862167108175329291155234133431256495186165800850480939395948647023937960370587015180526235807164349620200372082282153041480140456912677691184030985478987260144919138692599055396440254136094165144465177387897117241518119002151156994012940982185071384104913576348164605987962727398059082040045985921247609152298846513278146669552901243070877548
suspect3 = 19399106641059719430021192160300204748154013890459468255719373754354019167820792318092409182406115115530722200666728245446889796562750491115857160508014999883632529321252844540803747198849908691018558610987780941352925318030705567748409124616428965718613582321101358603980688505770743832166552232290945499674026703080355911673609019440196413604866135380765992660957896795208203543126720721831806050402994470347462682914357117859227310008496022278900904627608587245076871675416071315270832931533605319537498860164513939297842228067992324510225950750517047989392427879860701099273608883718222060264811834053566449919927
"""
suspect3 is just an RSA ciphertext, there is no interesting information we can obtain from it.
suspect2 is interesting however, because it tells us that $p^2 = \texttt{suspect2} - 1234 \;\text{ mod } q$ by Chinese remainder theorem.
Then from suspect1 we have $\texttt{suspect1} = (1234 p)^{4321} \;\text{ mod } q$. We can simplify this a bit: \[ \begin{align*} \texttt{suspect1} = (1234 p)^{4321} & = 1234^{4321} \cdot (p^2)^{2160} \cdot p \\ & = 1234^{4321} \cdot (\texttt{suspect2} - 1234)^{2160} \cdot p \;\text{ mod } q \end{align*} \] By squaring both sides, we can eliminate $p$: \[ \begin{align*} \texttt{suspect1}^2 & = (1234^{4321} \cdot (\texttt{suspect2} - 1234)^{2160})^2 \cdot p^2 \;\text{ mod } q \\ & = (1234^{4321} \cdot (\texttt{suspect2} - 1234)^{2160})^2 \cdot (\texttt{suspect2} - 1234) \;\text{ mod } q \\ & = 1234^{8642} \cdot (\texttt{suspect2} - 1234)^{4321} \;\text{ mod } q \end{align*} \] and this implies that $\texttt{suspect1}^2 - 1234^{8642} \cdot (\texttt{suspect2} - 1234)^{4321}$ is divisible by $q$.
contains_q = pow(1234, 8642, n) * pow(suspect2 - 1234, 4321, n) - suspect1**2
q = gcd(contains_q, n)
p = n//q
# print(p,q)
phi = (p-1)*(q-1)
d = inverse(e, phi)
flag = long_to_bytes(pow(suspect3, d, n))
print(flag)
# b'0xL4ugh{00ps_y0u_c4ught_r00t_me}'
Flag: 0xL4ugh{00ps_y0u_c4ught_r00t_me}
small eq’s
This was the one that struggled me the most (and the reason this writeup was so late).
(Writing in progress)
Updated: